��Ŀ����
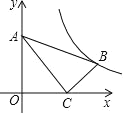
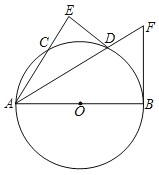
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���B����Ϊ��0��m����m��0������A��x���������ϣ�ֱ��AB������A��B����tan��BAO��2��
��1������A������Ϊ��3��0������ֱ��AB�ı���ʽ��
��2������������y��![]() ��ͼ����ֱ��AB���ڵ�һ����C��D���㣨BD��BC������AD��2DBʱ����k1��ֵ���ú�m��ʽ�ӱ�ʾ����
��ͼ����ֱ��AB���ڵ�һ����C��D���㣨BD��BC������AD��2DBʱ����k1��ֵ���ú�m��ʽ�ӱ�ʾ����
��3���ڣ�1���������£����߶�AB���е�ΪE������E��x��Ĵ��ߣ�����ΪM��������������y��![]() ��ͼ���ڵ�F���ֱ�����OE��OF������OEF���OBE����ʱ����ֱ��д������������k2ֵ��
��ͼ���ڵ�F���ֱ�����OE��OF������OEF���OBE����ʱ����ֱ��д������������k2ֵ��
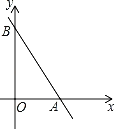
���𰸡���1��y����2x+6 ��2��4��3��![]() ��
��![]()
��������
��1����ͨ����ֱ�����������A�����꣬Ȼ����ݴ���ϵ�����������ֱ��AB�Ľ���ʽ��
��2����DE��OA����������ó�![]() �����DE����D�ĺ����꣬����AB�Ľ���ʽ��������꣬Ȼ����ݷ���������ͼ���ϵ�����������������k1��
�����DE����D�ĺ����꣬����AB�Ľ���ʽ��������꣬Ȼ����ݷ���������ͼ���ϵ�����������������k1��
��3�����ݹ��ɶ������AB��OE����һ�����BE��Ȼ��������������ε��������EF�ij����Ӷ����FM�ij����ó�F�����꣬Ȼ����ݷ���������ͼ���ϵ�����������������k2��
�⣺��1����A��3��0����B��0��m����m��0����
��OA��3��OB��m��
��tan��BAO��![]() ��2��
��2��
��m��6��
��ֱ��AB�Ľ���ʽΪy��kx+b��
����A��3��0����B��0��6���ã�![]() ��
��
��ã�b��6��k����2��
��ֱ��AB�Ľ���ʽΪy����2x+6��
��2����ͼ1��
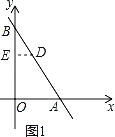
��AD��2DB��
��![]() ��
��
��DE��OA��
��![]() ��
��
��DE��![]() OA��1��
OA��1��
��D�ĺ�����Ϊ1��
����y����2x+6�ã�y��4��
��D��1��4����
��k1��1��4��4��
��3����ͼ2��
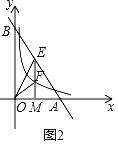
��A��3��0����B��0��6����
��E��![]() ��3����AB��
��3����AB��![]() ��
��
��OE��Rt��OABб���ϵ����ߣ�
��OE��![]() AB��
AB��![]() ��BE��
��BE��![]() ��
��
��EM��x�ᣬ
��F�ĺ�����Ϊ![]() ��
��
����OEF�ס�OBE��
��![]() ��
��![]() ��
��
��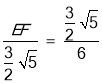 ��
��
��EF��![]() ��
��
��FM��3��![]() ��
��![]() ��
��
��F��![]() ��
��![]() ����
����
��k2��![]() ��
��![]() ��
��![]() ��
��
��ͼ3��
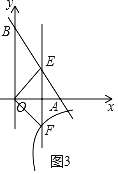
����OEF�ס�EOBʱ��
��![]() ��
��
��EF��OB��6��
��F��![]() ����3����
����3����
��k2����3��![]() ����
����![]() ��
��
��������������������k2ֵΪ![]() ��
��![]() ��
��