题目内容
【题目】如图,矩形ABCD中,AB=6,BC=3.点E在线段BA上从B点以每秒1个单位的速度出发向A点运动,F是射线CD上一动点,在点E、F运动的过程中始终保持EF=5,且CF>BE,点P是EF的中点,连接AP.设点E运动时间为ts.



(1)在点E、F运动的过程中,AP的长度存在一个最小值,当AP的长度取得最小值时,点P的位置应该在 .
(2)当AP⊥EF时,求出此时t的值
(3)以P为圆心作⊙P,当⊙P与矩形ABCD三边所在直线都相切时,求出此时t的值,并指出此时⊙P的半径长.
【答案】(1)AD的中点;(2)t=![]() (s);(3)
(s);(3)![]() ,
,![]() ;
;![]() ,
,![]()
【解析】
(1)在点E、F运动的过程中始终保持EF=5,且CF>BE,故EF在运动过程中始终保持平行移动,因为点P是EF的中点,则点P始终在过EF的中点且平行于AB的直线上运动,运动轨迹为一条线段,在运动过程中,根据垂线段最短可得P为AD的中点时,AP的长度最小;
(2)首先过点E作EG⊥CD于点G,易证得△APE∽△EGF,然后由相似三角形的对应边成比例,求得AE的长,继而求得答案;
(3)分两种情况考虑:当⊙P在矩形ABCD内分别与AB、AD、CD相切于点Q、R、N时,连接PQ,PR,PN,如图3所示,可得出四边形AQPR和四边形RPND为两个全等的正方形,其边长为大正方形边长的一半,在直角三角形PQE中,由PE与PQ的长,利用勾股定理求出EQ的长,进而由BA+AQ-EQ求出BE的长,即为t的值,并求出此时⊙P的半径;当⊙P在矩形ABCD外分别与射线BA、AD、射线CD相切于点Q、R、N时,如图4所示,同理求出BE的长,即为t的值,并求出此时⊙P的半径.
(1)在点E、F运动的过程中始终保持EF=5,且CF>BE,故EF在运动过程中始终保持平行移动,因为点P是EF的中点,则点P始终在过EF的中点且平行于AB的直线上运动,运动轨迹为一条线段,如图所示:根据垂线段最短可得P为AD的中点时,AP的长度最小;
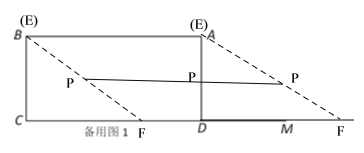
故答案为:AD的中点;
(2)过点E作EG⊥CD于点G,如图2
则四边形BCGE是矩形,
∴EG=BC=3,AB∥CD,
∴FG=![]() ,∠AEP=∠EFG
,∠AEP=∠EFG
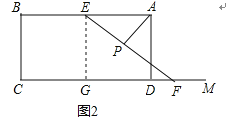
∵AP⊥EF,
∴∠APE=∠EGF=90°,
∴△APE∽△EGF,
∴ ![]()
∴
∴AE=![]()
∴BE=6-![]()
∴t=![]() (s)
(s)
(3)如图3,当⊙P在矩形ABCD内分别与AB、AD、CD相切于点Q、R、N时,
连接PQ、PR、PN,则PQ⊥AB、PR⊥AD、PN⊥CD,
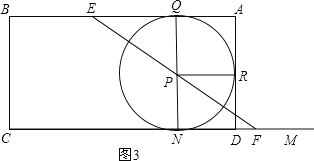
则四边形AQPR与四边形RPND为两个全等的正方形,
∴PQ=AQ=AR=DR=![]() AD=
AD=![]() ,
,
在Rt△PQE中,EP=![]() ,由勾股定理可得:EQ=2,
,由勾股定理可得:EQ=2,
∴BE=BA-EQ-AQ=6-2-![]() =
=![]() ,
,
∴t=![]() ,此时⊙P的半径为
,此时⊙P的半径为![]() ;
;
如图4,当⊙P在矩形ABCD外分别与射线BA、AD、射线CD相切于点Q、R、N时,
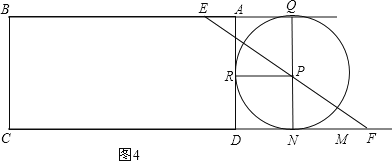
类比图3可得,EQ=2,AQ=![]() ,
,
∴BE=BA+AQ-EQ=6+![]() -2=
-2=![]() ,
,
∴t=![]() ,此时⊙P的半径为
,此时⊙P的半径为![]() .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】小明在“五一”假期间参加一项社会调查活动,在他所居住小区的600个家庭中,随机调查了50个家庭人均月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
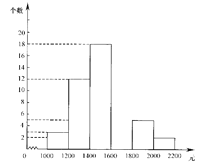
分 组 | 频 数 | 频 率 |
1000~1200 | 3 | 0.060 |
1200~1400 | 12 | 0.240 |
1400~1600 | 18 | 0.360 |
1600~1800 | 0.200 | |
1800~2000 | 5 | |
2000~2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
⑴ 补全频数分布表和频数分布直方图;
⑵ 这50个家庭人均月收入的中位数落在 小组;
⑶ 请你估算该小区600个家庭中人均月收入较低(不足1400元)的家庭个数大约有多少?