题目内容
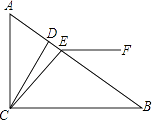
【题目】(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,![]() =
=![]() 时,求DE的长.
时,求DE的长.

【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)连接OD .根据EF与⊙O相切.可得OD⊥EF,所以要证明FE⊥AB,只要证明OD∥AB即可;
(2)首先利用sin∠CFD=![]() ,在Rt△AEF中,求出AF的长,然后利用△ODF∽△AEF.求出圆的半径,再根据EB=AB-AE计算即可.
,在Rt△AEF中,求出AF的长,然后利用△ODF∽△AEF.求出圆的半径,再根据EB=AB-AE计算即可.
试题解析:(1)证明:连接OD . (如图)
∵ OC=OD,
∴ ∠OCD="∠ODC."
∵ AB=AC,
∴∠ACB=∠B.
∴ ∠ODC=∠B.
∴ OD∥AB. 1分
∴ ∠ODF =∠AEF.
∵ EF与⊙O相切.
∴ OD⊥EF,∴ ∠ODF =90°.
∴∠AEF ="∠ODF" =90°.
∴ EF⊥AB. 2分
(2)解:由(1)知:OD∥AB,OD⊥EF .
在Rt△AEF中,sin∠CFD =![]() =
=![]() ,AE=6.
,AE=6.
∴ AF=10. 3分
∵ OD∥AB,
∴ △ODF∽△AEF.
∴![]() .
.
∴![]() .
.
解得r=![]() . 4分
. 4分
![]() ∴ AB=" AC=2r" =
∴ AB=" AC=2r" =![]() .
.
∴ EB=AB-AE=![]() -6=
-6=![]() . 5分
. 5分

练习册系列答案
相关题目