题目内容
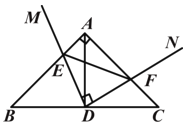
【题目】Rt△ ABC 中, AB=AC,点 D 为 BC 中点.∠ MDN=90°, ∠ MDN 绕点 D 旋转,DM、DN 分别与边 AB、AC 交于 E、F 两点.下列结论:① BE+CF=![]() BC;② S△AEF ≤
BC;② S△AEF ≤![]() S△ABC;③ S四边形AEDF=ADEF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
S△ABC;③ S四边形AEDF=ADEF;④ AD≥ EF;⑤ AD与EF可能互相平分,其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:先由ASA证明△AED≌△CFD,得出![]() ,再由勾股定理即可得出
,再由勾股定理即可得出![]() 从而判断①;设AB=AC=a,AE=CF=x,则AF=ax.先由三角形的面积公式得出
从而判断①;设AB=AC=a,AE=CF=x,则AF=ax.先由三角形的面积公式得出![]() 再根据二次函数的性质即可判断②;由勾股定理得到EF的表达式,利用二次函数性质求得EF最小值为
再根据二次函数的性质即可判断②;由勾股定理得到EF的表达式,利用二次函数性质求得EF最小值为![]() 而
而![]() 所以
所以![]() ,从而④错误;先得出
,从而④错误;先得出
S四边形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=![]() 再由
再由![]() 得到
得到![]()
∴ADEF>S四边形AEDF,所以③错误;如果四边形AEDF为平行四边形,则AD与EF互相平分,此时DF∥AB,DE∥AC,又D为BC中点,所以当E、F分别为AB、AC的中点时,AD与EF互相平分,从而判断⑤.
详解:∵Rt△ABC中,AB=AC,点D为BC中点,
∴![]() ,AD=BD=CD,
,AD=BD=CD,
∵![]()
∴![]()
∴∠ADE=∠CDF.
在△AED与△CFD中,
∵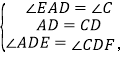
∴△AED≌△CFD(ASA),
∴AE=CF,
在Rt△ABD中,![]()
故①正确;
设AB=AC=a,AE=CF=x,则AF=ax.
∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]()
又∵![]()
∴![]()
故②正确;
![]()
∴当![]() 时,
时,![]() 取得最小值
取得最小值![]()
∴![]() (等号当且仅当
(等号当且仅当![]() 时成立),
时成立),
而![]() ∴
∴![]()
故④错误;
由①的证明知△AED≌△CFD,
∴S四边形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=![]() ,
,
∵![]()
∴![]()
∴ADEF>S四边形AEDF,
故③错误;
当E.F分别为AB、AC的中点时,四边形AEDF为正方形,此时AD与EF互相平分.
故⑤正确。
综上所述,正确的有:①②⑤,共3个.
故选C.

 黄冈创优卷系列答案
黄冈创优卷系列答案