题目内容
【题目】如图，抛物线y＝ax2＋bx＋c的对称轴是x＝－1．且过点（
，0），有下列结论：
①abc＞0；②a－2b＋4c＝0；③25a－10b＋4c＝0；④3b＋2c＞0；⑤a－bm≥（am－b）；其中所有正确的结论有（ ）个．
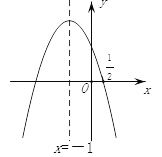
A. 2个 B. 3个 C. 4个 D. 5个
【答案】A
【解析】由抛物线的开口向下可得：a<0；
根据抛物线的对称轴在y轴左边可得：a，b同号，所以b<0；
根据抛物线与y轴的交点在正半轴可得：c>0，
∴abc>0，故①正确；
直线x=-1是抛物线y=ax2+bx+c（a≠0）的对称轴，所以
=-1，可得b=2a，a-2b+4c=a-4a+4c=-3a+4c，
∵a<0，c>0，
∴-3a+4c>0，
即a-2b+4c>0，故②错误；
∵抛物线y=ax2+bx+c的对称轴是x=-1．且过点（
，0），
∴抛物线与x轴的另一个交点坐标为（-
，0），
当x=-时，y=0，即a（-）2-b+c=0，
整理得：25a-10b+4c=0，故③正确；
∵b=2a，a+b+c<0，
∴b+b+c<0，
即3b+2c<0，故④错误；
a－bm≥（am－b）
a－bm－am+b≥0
a（1-m）+b（1-m）≥0，
（1-m）（a+b）≥0，
因a+b<0，当m=0时，上述式子不成立，所以⑤错误．
综上，正确的答案为：①③．故选A.
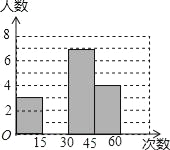
【题目】在大课间活动中，体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试，并对成绩进行统计分析，绘制了频数分布表和统计图，请你根据图表中的信息完成下列问题：
分 组 | 频数 | 频率 |
第一组（0≤x＜15） | 3 | 0.15 |
第二组（15≤x＜30） | 6 | a |
第三组（30≤x＜45） | 7 | 0.35 |
第四组（45≤x＜60） | b | 0.20 |
（1）频数分布表中a=_____，b=_____，并将统计图补充完整；
（2）如果该校七年级共有女生180人，估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人？
（3）已知第一组中只有一个甲班学生，第四组中只有一个乙班学生，老师随机从这两个组中各选一名学生谈心得体会，则所选两人正好都是甲班学生的概率是多少？
