题目内容
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC= ![]() ,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
,对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F. 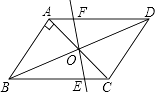
(1)证明:当∠AOF=90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,AF与CE总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时∠AOF度数.
【答案】
(1)当∠AOF=90°时,AB∥EF,
∵AF∥BE,
∴四边形ABEF是平行四边形
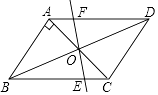
(2)证明:∵四边形ABEF是平行四边形,
∴AO=CO,AF∥EC,
∴∠FAO=∠ECO,
在△AOF和△COE中,
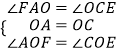 ,
,
∴△AOF≌△COE,
∴AF=CE.
(3)解:结论:四边形BEDF可能是菱形.
∵△AOF≌△COE,
∴OE=OF,
∴EF与BD互相平分,
∴四边形BEDF是平行四边形,
∴当EF⊥BD时,四边形BEDF是菱形,
在Rt△ABC中,AC= ![]() =2,
=2,
∴OA=1=AB,
∵AB⊥AC,
∴∠AOB=45°,
∴∠AOF=45°,
∴当四边形BEDF是菱形时,∠AOF=45°.
【解析】(1)根据两组对边分别平行的四边形是平行四边形即可证明.(2)只要证明△AOF≌△COE即可.(3)结论:四边形BEDF可能是菱形.根据菱形的对角线互相垂直即可解决问题.
【考点精析】掌握平行四边形的判定与性质和菱形的判定方法是解答本题的根本,需要知道若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

【题目】某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.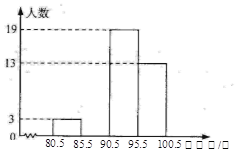
![]()