��Ŀ����
����Ŀ��ij��ѧ������1�����40��ͬѧ����һ��30���������������ǵijɼ�ͳ�����±���
������/�� | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
�� �� | 1 | 2 | 8 | 11 | 5 |
����Щ���ݰ����5���������飬���Ƴ���ͼ��Ƶ���ֲ�ֱ��ͼ������������
��1�������п�ȱ��������д����������ȫƵ���ֲ�ֱ��ͼ��
��2�������ͬѧ��������ɼ��������� ������λ���� ����
��3��������90���ɵ����֣�ѧУ�����꼶����720�ˣ��Թ��Ƹ���ѧ�����꼶���ж������������ܵ����֣�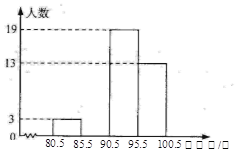
![]()
���𰸡�(1)�𰸼�����;(2) 95��95;.(3)54��.
�����������������(1)���ȸ���ֱ��ͼ�õ�95.5-100.5С�鹲��13��,��ͳ�Ʊ�֪����100������5��,�Ӷ������98��������;
(2)�����������λ���Ķ�����ռ���;
(3)�����������������弴�����.
���������
��1������ֱ��ͼ�õ�95.5��100.5С�鹲��13�ˣ���ͳ�Ʊ�֪����100������5�ˣ�
����98������13��5=8�ˣ�
��90������40��1��2��8��11��8��5=5�ˣ�
��ͳ�Ʊ�Ϊ��
������/�� | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
���� | 1 | 2 | 5 | 8 | 11 | 8 | 5 |
ֱ��ͼΪ��
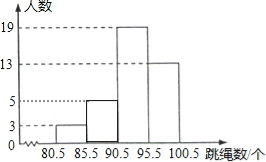
��2���۲�ͳ�Ʊ�֪������Ϊ95������λ��Ϊ95����
��3�����Ƹ���ѧ�����꼶���ܵ����ֵ���720![]() =54�ˣ�
=54�ˣ�

����Ŀ����ͼ,��������һ��������ķ��ͼ��ABCD,Ϊ����������,С���ڴ˷��ͼ���ڻ���һ���뾶Ϊ1 m��Բ��,�ڷ��ͼ��ABCD���������۾�����ͼ������Сʯ��(�ɰ�Сʯ�ӽ��ƿ��ɵ�),
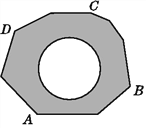
��¼����:
��Сʯ��������ܴ��� Сʯ���������Ч���� | 50 | 150 | 300 | �� |
Сʯ������Բ��(��Բ��)�Ĵ���m | 14 | 48 | 89 | �� |
Сʯ������Բ�������Ӱ����(����Ե)�Ĵ���n | 30 | 95 | 180 | �� |
(1)��Ͷ���Ĵ����ܴ�ʱ,m��n��ֵԽ��Խ�ӽ�___________(�����ȷ��0.1);
(2)����Сʯ���������Ч������Ĵ���Ϊ����(��m+n),������Ͷ������������,Сʯ������Բ��(��Բ��)��Ƶ���ȶ���___________����;
(3)����Ͷһ��ʯ��,��Сʯ������Բ��(��Բ��)�ĸ���Ϊ___________;
(4)��������(2)������Ƶ��,�����������ͼ��ABCD������Ƕ���ƽ����(���������).