题目内容
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40cm. 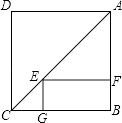
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
【答案】
(1)证明:∵四边形ABCD为正方形,
∴AB⊥BC,∠B=90°.
∵EF⊥AB,EG⊥BC,
∴EF∥GB,EG∥BF.
∵∠B=90°,
∴四边形BFEG是矩形
(2)解:∵正方形ABCD的周长是40cm,
∴AB=40÷4=10cm.
∵四边形ABCD为正方形,
∴△AEF为等腰直角三角形,
∴AF=EF,
∴四边形EFBG的周长C=2(EF+BF)=2(AF+BF)=20cm
(3)解:若要四边形BFEG是正方形,只需EF=BF,
∵AF=EF,AB=10cm,
∴当AF=5cm时,四边形BFEG是正方形
【解析】(1)由正方形的性质可得出AB⊥BC、∠B=90°,根据EF⊥AB、EG⊥BC利用“垂直于同一条直线的两直线互相平行”,即可得出EF∥GB、EG∥BF,再结合∠B=90°,即可证出四边形BFEG是矩形;(2)由正方形的周长可求出正方形的边长,根据正方形的性质可得出△AEF为等腰直角三角形,进而可得出AF=EF,再根据矩形的周长公式即可求出结论;(3)由正方形的判定可知:若要四边形BFEG是正方形,只需EF=BF,结合AF=EF、AB=10cm,即可得出结论.

练习册系列答案
相关题目