题目内容
平面直角坐标系xOy中,抛物线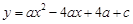 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3)在(1)的条件下,对于实数c、d,我们可用min{ c,d }表示c、d两数中较小的数,如min{3,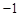 }=
}=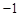 .若关于x的函数y = min{
.若关于x的函数y = min{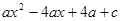 ,
,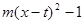
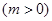 }的图象关于直线
}的图象关于直线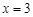 对称,试讨论其与动直线
对称,试讨论其与动直线 交点的个数。
交点的个数。
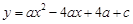 与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D. (1)求此抛物线的解析式;
(2)若此抛物线的对称轴上的点P满足∠APB=∠ACB,求点P的坐标;
(3)在(1)的条件下,对于实数c、d,我们可用min{ c,d }表示c、d两数中较小的数,如min{3,
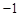 }=
}=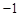 .若关于x的函数y = min{
.若关于x的函数y = min{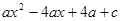 ,
,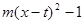
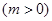 }的图象关于直线
}的图象关于直线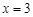 对称,试讨论其与动直线
对称,试讨论其与动直线 交点的个数。
交点的个数。(1)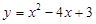 ;(2)
;(2)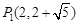 、
、 ;
;
(3)当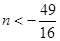 时,动直线
时,动直线 与函数图象无交点;
与函数图象无交点;
当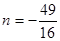 时,动直线
时,动直线 与函数图象有唯一的一个交点;
与函数图象有唯一的一个交点;
当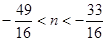 时,动直线
时,动直线 与函数图象有两个交点;
与函数图象有两个交点;
当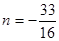 时,动直线
时,动直线 与函数图象有三个交点;
与函数图象有三个交点;
当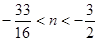 时,动直线
时,动直线 与函数图象有四个交点;
与函数图象有四个交点;
当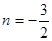 时,动直线
时,动直线 与函数图象有三个交点;
与函数图象有三个交点;
当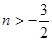 时,动直线
时,动直线 与函数图象有三个交点.
与函数图象有三个交点.
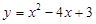 ;(2)
;(2)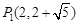 、
、 ;
;(3)当
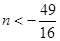 时,动直线
时,动直线 与函数图象无交点;
与函数图象无交点;当
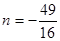 时,动直线
时,动直线 与函数图象有唯一的一个交点;
与函数图象有唯一的一个交点;当
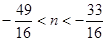 时,动直线
时,动直线 与函数图象有两个交点;
与函数图象有两个交点;当
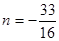 时,动直线
时,动直线 与函数图象有三个交点;
与函数图象有三个交点;当
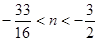 时,动直线
时,动直线 与函数图象有四个交点;
与函数图象有四个交点;当
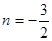 时,动直线
时,动直线 与函数图象有三个交点;
与函数图象有三个交点;当
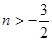 时,动直线
时,动直线 与函数图象有三个交点.
与函数图象有三个交点.试题分析:(1)首先将已知的抛物线解析式进行配方,得出对称轴方程后结合A点坐标可确定B点的坐标,由OB=OC的条件能得到C点坐标,利用待定系数法即可确定函数的解析式.
(2)此题需要进行适当转化,首先作△ABC的外切圆,根据圆周角定理可知:P点应为抛物线对称轴与⊙E的交点,那么只需求出圆心E的坐标和⊙E的半径即可得到P点坐标.首先由A、B的坐标可确定F点的坐标以及AF的长,而弦BC的垂直平分线过点E,由此可确定该中垂线的解析式,进一步可确定点E的坐标;然后在Rt△AEF中,通过解直角三角形可得到圆的半径长,由此求出全部条件;
(3)由题意可知所求得的函数的解析式为
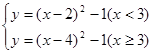 ,由函数图象分
,由函数图象分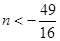 、
、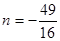 、
、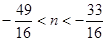 、
、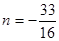 、
、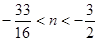 、
、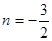 、
、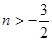 等情况分析.
等情况分析.(1)∵
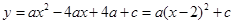 ,
,∴ 抛物线的对称轴为直线
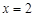 .
.∵ 抛物线
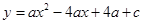 与x轴交于
与x轴交于点A、点B,点A的坐标为
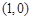 ,
,∴ 点B的坐标为
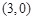 ,OB=3.
,OB=3.可得该抛物线的解析式为
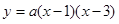 .
.∵ OB=OC,抛物线与y轴的正半轴交于点C,
∴ OC=3,点C的坐标为
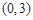 .
.将点C的坐标代入该解析式,解得a=1.
∴ 此抛物线的解析式为
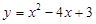 .
.(2)作△ABC的外接圆☉E,设抛物线的对称轴与x轴的交点为点F,设☉E与抛物线的对称轴位于x轴上方的部分的交点为点
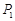 ,点
,点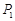 关于x轴的对称点为点
关于x轴的对称点为点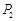 ,点
,点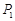 、点
、点 均为所求点.
均为所求点.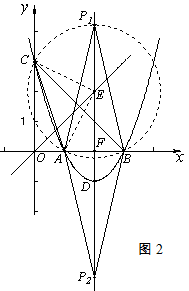
可知圆心E必在AB边的垂直平分线即抛物线的对称轴直线
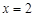 上.
上. ∵
 、
、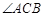 都是弧AB所对的圆周角,
都是弧AB所对的圆周角,∴
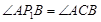 ,且射线FE上的其它点P都不满足
,且射线FE上的其它点P都不满足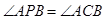 .
.由(1)可知 ∠OBC=45°,AB=2,OF=2.
可得圆心E也在BC边的垂直平分线即直线
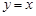 上.
上.∴ 点E的坐标为
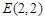 .
.∴ 由勾股定理得
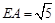 .
.∴
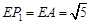 .
.∴ 点
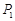 的坐标为
的坐标为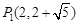 .
.由对称性得点
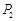 的坐标为
的坐标为 .
.∴符合题意的点P的坐标为
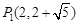 、
、 .
.(3)由题意可知,原二次函数的解析式为
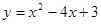 可得,
可得,所求得的函数的解析式为
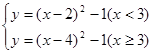
由函数图象可知:当
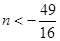 时,动直线
时,动直线 与函数图象无交点;
与函数图象无交点;当
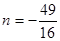 时,动直线
时,动直线 与函数图象有唯一的一个交点;
与函数图象有唯一的一个交点;当
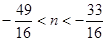 时,动直线
时,动直线 与函数图象有两个交点;
与函数图象有两个交点;当
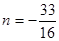 时,动直线
时,动直线 与函数图象有三个交点;
与函数图象有三个交点;当
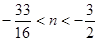 时,动直线
时,动直线 与函数图象有四个交点;
与函数图象有四个交点;当
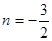 时,动直线
时,动直线 与函数图象有三个交点;
与函数图象有三个交点;当
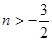 时,动直线
时,动直线 与函数图象有三个交点.
与函数图象有三个交点.点评:这道二次函数题由于融合了圆、解直角三角形、轴对称图形等重点知识,难度较大;(2)中,将角相等转化为圆的相关问题是打开解题突破口的关键,应注意并总结转化思想在解题中的妙用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 经过(2,1)和(6,-5)两点.
经过(2,1)和(6,-5)两点.
 右侧的此抛物线上一点,过点P作PM
右侧的此抛物线上一点,过点P作PM
 轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标; 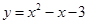 经过点
经过点 、
、 ,则
,则 与
与 的大小关系是_______.
的大小关系是_______. 的最大值是 .
的最大值是 . ,0)、(3,0)两点,则下列判断中,错误的是
,0)、(3,0)两点,则下列判断中,错误的是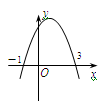

 、
、 ,那么在这次比赛中,成绩较好的学生是( )
,那么在这次比赛中,成绩较好的学生是( ) 的图象如图所示,则一次函数
的图象如图所示,则一次函数 与反比例函数
与反比例函数 在同一坐标系内的图象可能为 ( )
在同一坐标系内的图象可能为 ( )