题目内容
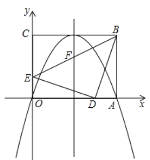
【题目】已知二次函数
的图象
经过
， 
两点.
（1）求
对应的函数表达式；
（2）将
先向左平移1个单位，再向上平移4个单位，得到抛物线
，将
对应的函数表达式记为
，求
对应的函数表达式；
（3）设
，在（2）的条件下，如果在
≤x≤a内存在某一个x的值，使得
≤
成立，根据函数图象直接写出a的取值范围.
【答案】（1）
；（2）
；（3）a≥
.
【解析】试题分析：（1）根据待定系数法，可得函数解析式；
（2）根据抛物线平移的规律：向左平移加，向上平移加，可得答案；
（3）根据函数与不等式的关系，可得答案．
试题解析：解：（1）∵二次函数
的图象
经过
， 
两点，∴
，解得
，∴抛物线
的函数表达式为
；
（2）∵
，∴抛物线的顶点为
，∴平移后抛物线
的顶点为
，它对应的函数表达式为
；
（3）
（见图）．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
【题目】如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=6cm，设弦AP的长为xcm，△APO的面积为ycm2，（当点P与点A或点B重合时，y的值为0）．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整；
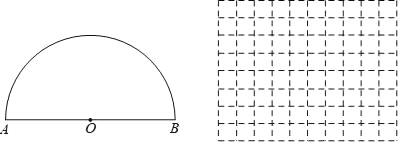
（1）通过取点、画图、测量、计算，得到了x与y的几组值，如下表：
x/cm | 0.5 | 1 | 2 | 3 | 3.5 | 4 | 5 | 5.5 | 5.8 |
y/cm2 | 0.8 | 1.5 | 2.8 | 3.9 | 4.2 | m | 4.2 | 3.3 | 2.3 |
那么m= ；（保留一位小数）
（2）建立平面直角坐标系，描出以表中各组对应值为坐标的点，画出该函数图象．
（3）结合函数图象说明，当△APO的面积是4时，则AP的值约为 ．（保留一位小数）
