题目内容
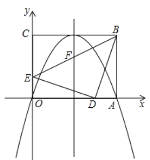
【题目】如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）.
（1）求抛物线的解析式；
（2）猜想△EDB的形状并加以证明.
【答案】（1）y=—
x2+3x；（2）△EDB为等腰直角三角形，见解析.
【解析】
（1）由条件可求得抛物线的顶点坐标及A点坐标，利用待定系数法可求得抛物线解析式；
（2）由B、D、E的坐标可分别求得DE、BD和BE的长，再利用勾股定理的逆定理可进行判断；
（1）在矩形OABC中，OA=4，OC=3，
∴A（4，0），C（0，3），
∵抛物线经过O、A两点，顶点在BC边上，
∴抛物线顶点坐标为（2，3），
∴可设抛物线解析式为y=a（x﹣2）2+3，
把A点坐标代入可得0=a（4﹣2）2+3，解得a=－，
∴抛物线解析式为y=—（x﹣2）2+3，即y=—x2+3x；
（2）△EDB为等腰直角三角形．
证明：
由（1）可知B（4，3），且D（3，0），E（0，1），
∴DE2=32+12=10，BD2=（4﹣3）2+32=10，BE2=42+（3﹣1）2=20，
∴DE2+BD2=BE2，且DE=BD，
∴△EDB为等腰直角三角形.
轻松夺冠全能掌控卷系列答案
【题目】从北京市环保局证实，为满足2022年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．过程如下，请补充完整．
收集数据：
从2016年12月初开始，连续一年对两镇的空气质量进行监测（将30天的空气污染指数（简称：API）的平均值作为每个月的空气污染指数，12个月的空气污染指数如下：
千家店镇：120 115 100 100 95 85 80 70 50 50 50 45
永宁 镇：110 90 105 80 90 85 90 60 90 45 70 60
整理、描述数据：
空气质量
按如表整理、描述这两镇空气污染指数的数据：
空气质量为优 | 空气质量为良 | 空气质量为轻微污染 | |
千家店镇 | 4 | 6 | 2 |
永宁 镇 |
|
|
|
（说明：空气污染指数≤50时，空气质量为优；50＜空气污染指数≤100时，空气质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．）
分析数据：
两镇的空气污染指数的平均数、中位数、众数如下表所示；
城镇 | 平均数 | 中位数 | 众数 |
千家店 | 80 |
| 50 |
永 宁 | 81.3 | 87.5 |
|
请将以上两个表格补充完整；
得出结论：可以推断出 镇这一年中环境状况比较好，理由为 ．（至少从两个不同的角度说明推断的合理性）
