题目内容
【题目】平行四边形
中，对角线
， 
相交于点
，若
、
是
两动点， 
、
分别从
、
两点同时以2cm/s的相同的速度向
、
运动。
(1)四边形
是平行四边形吗?说明你的理由。
(2)若
cm， 
cm，当运动时间
为多少时，以
、
、
、
为顶点的四边形为矩形。
【答案】(1)四边形
是平行四边形，理由见解析；
(2)当运动时间为2s或7s多少时，以
、
、
、
为顶点的四边形为矩形.
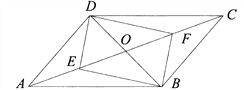
【解析】试题解析：（1）由平行四边形ABCD中，可得OA=OC，OB=OD，又由若E、F是AC上两动点，E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动，易得AE=CF，即可得OE=OF，则可判定四边形DEBF是平行四边形；
（2）由四边形DEBF是平行四边形，可得当EF=BD时，四边形DEBF为矩形，即可得方程：18-2t-2t=10，继而求得答案．
试题解析：（1）四边形DEBF是平行四边形．
理由：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵E、F是AC上两动点，E、F分别从A、C两点同时以2cm/s的相同的速度向C、A运动，
∴AE=CF，
∴OE=OF，
∴四边形DEBF是平行四边形；
（2）根据题意得：AE=CF=2tcm或18-2tcm，
∵四边形DEBF是平行四边形，
∴当EF=BD时，四边形DEBF为矩形．
即AC-AE-CF=BD或AE+CF-AC=EF，
∴18-2t-2t=10或2t+2t-18=10，
解得：t=2或t=7
∴当运动时间t为2s或7s时，四边形DEBF为矩形．
练习册系列答案
相关题目
