题目内容
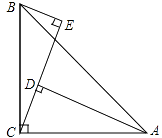
【题目】如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°. 
(1)求∠DAC的度数;
(2)求证:DC=AB.
【答案】
(1)解:∵AB=AC,
∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°,
∴∠BAC=180°﹣30°﹣30°=120°,
∵∠DAB=45°,
∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°
(2)证明:∵∠DAB=45°,
∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,
∴DC=AC,
∴DC=AB
【解析】(1)由AB=AC,根据等腰三角形的两底角相等得到∠B=∠C=30°,再根据三角形的内角和定理可计算出∠BAC=120°,而∠DAB=45°,则∠DAC=∠BAC﹣∠DAB=120°﹣45°;(2)根据三角形外角性质得到∠ADC=∠B+∠DAB=75°,而由(1)得到∠DAC=75°,再根据等腰三角形的判定可得DC=AC,这样即可得到结论.
【考点精析】关于本题考查的等腰三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目