题目内容
已知在锐角△ABC中,I是△ABC三条角平分线的交点,IG⊥BC于G,试比较∠1与∠2的大小,并说明理由.
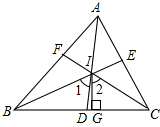

∠1=∠2.
理由:∵BE、AD、CF是角平分线
∴∠ABE=
∠ABC,∠BAD=
∠BAC,∠BCF=
∠BCA,
∴∠BID=∠ABE+∠BAD
=
∠ABC+
∠BAC
=
(∠ABC+∠BAC)
=
(180°-∠ACB)
=90°-
∠ACB
=90°-∠BCF
=90°-∠GCI
∵ID⊥BC
∴∠CIG=90°-∠GCI
∴∠BID=∠CIG,即∠1=∠2.
理由:∵BE、AD、CF是角平分线
∴∠ABE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BID=∠ABE+∠BAD
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
=90°-∠BCF
=90°-∠GCI
∵ID⊥BC
∴∠CIG=90°-∠GCI
∴∠BID=∠CIG,即∠1=∠2.

练习册系列答案
相关题目