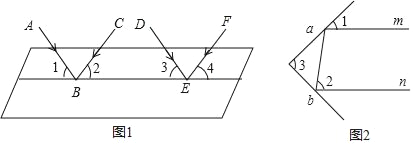
题目内容
【题目】下列命题中是真命题的是（ ）
A. 两条对角线相等的四边形是矩形；
B. 有一条对角线平分一个内角的平行四边形为菱形；
C. 对角线互相垂直且相等的四边形是正方形；
D. 依次连结四边形各边的中点，所得四边形是菱形．
【答案】B
【解析】分析：根据菱形、矩形和正方形的判定来逐一分析各个选项，从而选出正确的答案.
详解：A. ∵两条对角线相等的四边形可能是等腰梯形，故A不正确；
B. 有一条对角线平分一个内角的平行四边形为菱形，正确；
如图，四边形ABCD是平行四边形，BD平分∠ABC.
求证：四边形ABCD是菱形.
证明：∵四边形ABCD是平行四边形，
∴AD∥BC,
∴∠2=∠3.
∵BD平分∠ABC,
∴∠1=∠2,
∴∠1=∠3,
∴AB=AD,
∴四边形ABCD是菱形.
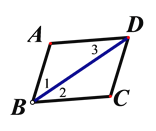
C. ∵对角线互相垂直且相等的四边形可能是筝形，故C不正确；
D. ∵依次连结四边形各边的中点，所得四边形是平行四边形，故D不正确．
练习册系列答案
相关题目
【题目】为了庆祝即将到来的“五四”青年节，某校举行了书法比赛，赛后随机抽查部分参赛同学的成绩，并制作成图表如下：
分数段 | 频数 | 频率 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | m | 0.45 |
80≤x＜90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息，解答下列问题：
（1）这次随机抽查了 名学生；表中的数m= ，n= ；
（2）请在图中补全频数分布直方图；
（3）若绘制扇形统计图，分数段60≤x＜70所对应扇形的圆心角的度数是 ；
（4）全校共有600名学生参加比赛，估计该校成绩80≤x＜100范围内的学生有多少人？
