��Ŀ����
����Ŀ����1���Ķ����ش�
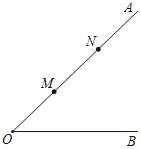
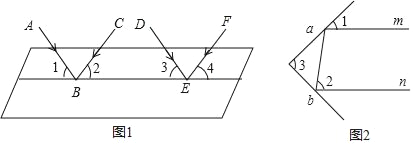
��ѧʵ��֤����ƽ�澵������ߵĹ����ǣ��䵽ƽ�澵�ϵĹ��ߺͱ�������Ĺ�����ƽ�澵���еĽ���ȣ���ͼ1��һ��ƽ�й���AB��DE����һ��ˮƽ������䣬��ʱ��1=��2����3=��4��
��������֪����1����3�Ĵ�С��ϵ���� ������������ ������2����4�Ĵ�С��ϵ���� ����
�������BC��EF��λ�ù�ϵ���� ������������ ����
��2��������⣺
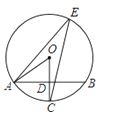
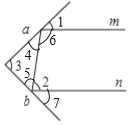
����ͼ2��һ������m�䵽ƽ�澵a�ϣ���a���䵽ƽ�澵b�ϣ��ֱ�b�����䣬��b������Ĺ���nƽ����m������1=35��������2=�� ������3=�� ����
����������1=40��������3=�� ����
���٢�������룺����3=�� ��ʱ���κ��䵽ƽ�澵a�ϵĹ���m����ƽ�澵a��b�����η�����������m�뷴�����n����ƽ�еģ���˵�����ɣ�
���𰸡���1������ȡ���ֱ��ƽ�У�ͬλ����ȡ���ȣ���ƽ�С�ͬλ����ȣ���ֱ��ƽ�У���2����70�㡢90�㣻��90�㣻��90�㣮
��������
��1������ƽ���ߵ��ж���������һ��⣻
��2���ٸ�������ǵ��ڷ���ǵó���1=��4����5=��7�������6������ƽ�������ʼ��������2�������5�������������ڽǺ������3���ɣ�
�����ͬ����
�������4+��5�������1+��4+��5+��7�����������2+��6������ƽ���ߵ��ж��Ƴ����ɣ�
��1������������֪����1����3�Ĵ�С��ϵ����ȣ���������ֱ��ƽ�У�ͬλ����ȣ���2����4�Ĵ�С��ϵ����ȣ�
���������BC��EF��λ�ù�ϵ��ƽ�У�������ͬλ����ȣ���ֱ��ƽ�У�
�ʴ�Ϊ������ȡ���ֱ��ƽ�У�ͬλ����ȡ���ȣ���ƽ�С�ͬλ����ȣ���ֱ��ƽ�У�
��2������ͼ��
�ߡ�1=35�㣬
���4=��1=35�㣬
���6=180�㩁35�㩁35��=110�㣬
��m��n��
���2+��6=180�㣬
���2=70�㣬
���5=��7=55�㣬
���3=180�㩁55�㩁35��=90�㣻
�������У�����1=40��������4=��1=40�㣬
���6=180�㩁40�㩁40��=100�㣬
��m��n��
���2+��6=180�㣬
���2=80�㣬
���5=��7=50�㣬
���3=180�㩁50�㩁40��=90��.
�����룺����3=90��ʱ��m��ƽ����n��
���ɣ��������ε��ڽǺ�Ϊ180��������3=90�㣬

���4+��5=90��.
�ߡ�4=��1����5=��7��
���1+��7=90�㣬
���1+��4+��5+��7=90��+90��=180�㣬
�ߡ�1+��4+��6+��5+��2+��7=180��+180��=360�㣬
���6+��2=180��.
��m��n��ͬ���ڽǻ�������ֱ��ƽ�У�.
�ʴ�Ϊ����70�㡢90�㣻��90�㣻��90�㣮

 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�