题目内容
【题目】已知:以O为圆心的扇形AOB中,∠AOB=90°,点C为 ![]() 上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.
上一动点,射线AC交射线OB于点D,过点D作OD的垂线交射线OC于点E,联结AE.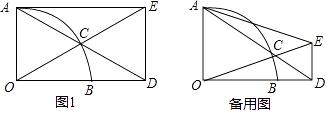
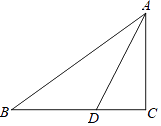
(1)如图1,当四边形AODE为矩形时,求∠ADO的度数;
(2)当扇形的半径长为5,且AC=6时,求线段DE的长;
(3)联结BC,试问:在点C运动的过程中,∠BCD的大小是否确定?若是,请求出它的度数;若不是,请说明理由.
【答案】
(1)解:如图1中,

∵四边形ABCD是矩形,
∴AD=EC,AC=CD,OC=CE,∠AOD=90°
∴AC=OC=OA,
∴△AOC是等边三角形,
∴∠OAD=60°,
∴∠ADO=90°﹣∠OAD=30°.
(2)解:如图2中,作OH⊥AD于H.
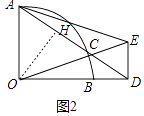
∵OA=OC,OH⊥AC,
∴AH=HC=3,
∵∠OAH=∠OAD,∠AHO=∠AOD,
∴△AOH∽△ADO,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AD= ![]() ,
,
∴CD=AD﹣AC= ![]() ,
,
∵DE⊥OD,
∴∠EDO=90°,
∴∠AOD+∠EDO=180°,
∴DE∥OA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DE= ![]() .
.
(3)解:如图3中,结论:∠BCD的值是确定的.∠BCD=45°.
理由:连接AB、BC.
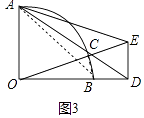
∵∠BCD=∠BAC+∠ABC,
又∵∠BAC= ![]() ∠BOC,∠ABC=
∠BOC,∠ABC= ![]() ∠AOC,
∠AOC,
∴∠BCD= ![]() ∠BOC+
∠BOC+ ![]() ∠AOC=
∠AOC= ![]() (∠BCO+∠AOC)=
(∠BCO+∠AOC)= ![]() ×90°=45°.
×90°=45°.
【解析】(1)利用矩形的性质,只要证明△OAC是等边三角形即可求解题中问题;(2)作OH⊥AD于H.由△AOH∽△ADO,推出![]() =
=![]() ,可得AD的长度,CD=AD﹣AC的长度,由DE∥OA,可得
,可得AD的长度,CD=AD﹣AC的长度,由DE∥OA,可得![]() =
=![]() ,即可求出DE;(3)结论:∠BCD的值是确定的.∠BCD=45°.连接AB、BC.由∠BCD=∠BAC+∠ABC,又∠BAC=
,即可求出DE;(3)结论:∠BCD的值是确定的.∠BCD=45°.连接AB、BC.由∠BCD=∠BAC+∠ABC,又∠BAC= ![]() ∠BOC,∠ABC=
∠BOC,∠ABC= ![]() ∠AOC,即可得出结论。
∠AOC,即可得出结论。
【考点精析】掌握矩形的性质和平行线分线段成比例是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;三条平行线截两条直线,所得的对应线段成比例.

【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?