Question

如图，在梯形ABCD中，AD∥BC，E为BC的中点，BC=2AD，EA=ED=2，AC与ED相交于点F．
（1）求证：梯形ABCD是等腰梯形；
（2）当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由，并求出此时菱形AECD的面积．

Answer 1

（1）证明：∵AD∥BC，
∴∠DEC=∠EDA，∠BEA=∠EAD，
又∵EA=ED，
∴∠EAD=∠EDA，
∴∠DEC=∠AEB，
又∵EB=EC，
∴△DEC≌△AEB，
∴AB=CD，
∴梯形ABCD是等腰梯形．

（2）当AB⊥AC时，四边形AECD是菱形．
证明：∵AD∥BC，BE=EC=AD，
∴四边形ABED和四边形AECD均为平行四边形．
∴AB

∥

.

ED，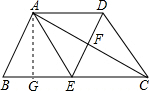
∵AB⊥AC，
∴AE=BE=EC，
∴平行四边形AECD是菱形．
过A作AG⊥BE于点G，
∵AE=BE=AB=2，
∴△ABE是等边三角形，
∴∠AEB=60°，
∴AG=

3

，
∴S_菱形AECD=EC•AG=2×

3

=2

3

．