Question

【题目】如图，在△ABC中，AC＝BC，∠ACB＝90°，⊙O（圆心O在△ABC内部）经过B、C两点，并交AB于点E，过点E作⊙O的切线交AC于点F．延长CO交AB于点G，作ED∥AC交CG于点D.

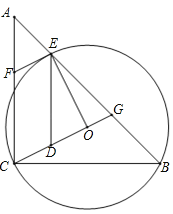
（1）求证：四边形CDEF是平行四边形；

（2）若BC＝3，＝2，求BG的值．

Answer 1

【答案】（1）见解析；（2）BG＝．

【解析】

（1）先证明∠COE＝2∠B＝90°，根据EF是⊙O的切线，得到EF∥OC，又DE∥CF，可得到四边形CDEF是平行四边形；

（2）过G作GN⊥BC于N

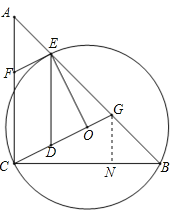
tan∠EDO＝tan∠CGN＝＝2，CN＝2GN，CN+BN＝2GN+GN＝3，GN＝1，得到

BG＝GN＝．

（1）∵在△ABC中，AC＝BC，∠ACB＝90°，

∴∠B＝45°，

∴∠COE＝2∠B＝90°，

∵EF是⊙O的切线，

∴∠FEO＝90°，

∴EF∥OC，

∵DE∥CF，

∴四边形CDEF是平行四边形；

（2）过G作GN⊥BC于N．

∴△GNB是等腰直角三角形，

∴NB＝GN，

∵四边形CDEF是平行四边形，

∴∠FCD＝∠FED，

∵∠ACD+∠GCB＝∠GCB+∠CGN＝90°，

∴∠CGN＝∠ACD，

∴∠CGN＝∠DEF，

∵＝2，

∴tan∠EDO＝tan∠CGN＝＝2，

∴CN＝2GN，

∴CN+BN＝2GN+GN＝3，

∴GN＝1，

∴BG＝GN＝．