题目内容
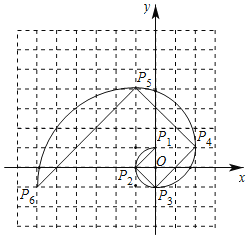
【题目】如图,已知直线y=ax+b与双曲线y=![]() (x>0)交于A(x1,y1),B(x2,y2)两点,点A与点B不重合,直线AB与x轴交于点P(x0,0),与y轴交于点C.
(x>0)交于A(x1,y1),B(x2,y2)两点,点A与点B不重合,直线AB与x轴交于点P(x0,0),与y轴交于点C.
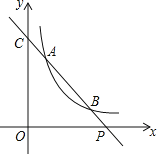
(1)若A、B两点坐标分别为(1,4),(4,y2),求点P的坐标;
(2)若b=y1+1,x0=6,且y1=2y2,求A,B两点的坐标;
(3)若将(1)中的点A,B绕原点O顺时针旋转90°,A点对应的点为A′,B点的对应点为B′点,连接AB′,A′B′,动点M从A点出发沿线段AB′以每秒1个单位长度的速度向终点B′运动;动点N同时从B′点出发沿线段B′A′以每秒1个单位长度的速度向终点A′运动,当其中一个点停止运动时另一个点也随之停止运动.设运动的时间为t秒,试探究:是否存在使△MNB′为等腰直角三角形的t值,若存在,求出t的值;若不存在,说明理由.
【答案】(1)P(5,0);(2)A(2,2),B(4,1);(3)存在,t的值为8![]() ﹣8或16﹣8
﹣8或16﹣8![]() .
.
【解析】
(1)先把A(1,3)),B(3,y2)代入y=![]() 求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出![]() ,
,![]() ,根据题意得出
,根据题意得出![]() ,
,![]() ,从而求得B(
,从而求得B(![]() y1),然后根据k=xy得出x1y1=
y1),然后根据k=xy得出x1y1=![]() y1,求得x1=2,代入
y1,求得x1=2,代入![]() ,解得y1=2,即可求得A、B的坐标;
,解得y1=2,即可求得A、B的坐标;
(3)如图2,根据旋转的性质得到B′(1,-4),求得AB′=8,求得AM=BN=t,B′M=8-t,①当∠B′N1M1=90°,②当∠B′M2N2=90°,根据等腰直角三角形的性质即可得到结论.
(1)∵直线y=ax+b与双曲线y=![]() (x>0)交于A(1,4)
(x>0)交于A(1,4)
∴k=1×4=4,
∴y=![]() ,
,
∵B(4,y2)在反比例函数的图象上,
∴y2=![]() =1,
=1,
∴B(4,1),
∵直线y=ax+b经过A、B两点,
∴![]() ,解得
,解得![]() ,
,
∴直线为y=-x+5,
令y=0,则x=5,
∴P(5,0);
(2)如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,

则AD∥BG∥x轴,AE∥BF∥y轴,
∴![]() ,
,
∵b=y1+1,y1=2y2,
∴![]() ,
,![]() ,
,
∴B(![]() y1),∵A,B两点都是反比例函数图象上的点,
y1),∵A,B两点都是反比例函数图象上的点,
∴x1y1=![]() y1,
y1,
解得x1=2,
代入![]() ,解得y1=2,
,解得y1=2,
∴A(2,2),B(4,1);
(3)存在,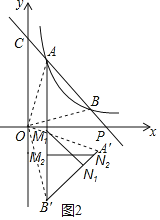
如图2,∵A、B两点坐标分别为(1,4),(4,1),将B绕原点O顺时针旋转90°,
∴B′(1,-4),
∴AB′=8,
由题意得:AM=BN=t,
∴B′M=8-t,
∵△MNB′为等腰直角三角形,
∴①当∠B′N1M1=90°,即B′M1=![]() B′N1,
B′N1,
∴8-t=![]() t,
t,
解得:t=8![]() -8;
-8;
②当∠B′M2N2=90°,即B′N2=![]() B′M2,
B′M2,
∴t=![]() (8-t),
(8-t),
解得:t=16-8![]() ;
;
综上所述,t的值为8![]() -8或16-8
-8或16-8![]() .
.