Question

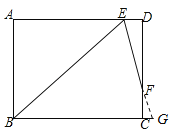
【题目】在矩形ABCD中，∠B的角平分线BE与AD交于点E，∠BED的角平分线EF与DC交于点F，若AB=9，DF=2FC，则BC= ．（结果保留根号）

Answer 1

【答案】．

【解析】

试题分析：延长EF和BC，交于点G．∵矩形ABCD中，∠B的角平分线BE与AD交于点E，∴∠ABE=∠AEB=45°，∴AB=AE=9，∴直角三角形ABE中，BE==，又∵∠BED的角平分线EF与DC交于点F，∴∠BEG=∠DEF．

∵AD∥BC，∴∠G=∠DEF，∴∠BEG=∠G，∴BG=BE=．

由∠G=∠DEF，∠EFD=∠GFC，可得△EFD∽△GFC，∴.

设CG=x，DE=2x，则AD=9+2x=BC．

∵BG=BC+CG，∴=9+2x+x，解得x=，∴BC=9+2（）=．

故答案为：．