题目内容
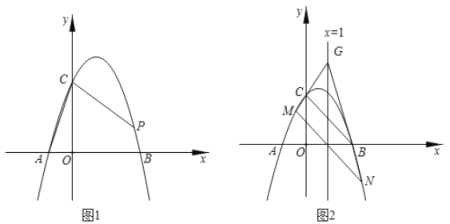
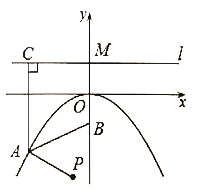
【题目】如图,抛物线![]() 经过点
经过点![]() .点
.点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 于点
于点![]() .
.
![]() 求抛物线解析式:
求抛物线解析式:
![]() 在抛物线对称轴上是否存在一定点
在抛物线对称轴上是否存在一定点![]() ,使得
,使得![]() 永远成立?若存在,求出点
永远成立?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)在抛物线对称轴上存在一定点
;(2)在抛物线对称轴上存在一定点![]() ,使得
,使得![]() 永远成立,点
永远成立,点![]() 坐标为
坐标为![]() ;(3)
;(3)![]()
【解析】
(1)把点![]() 代入
代入![]() 即可求出a的值;
即可求出a的值;
(2)设点![]() 坐标为
坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,得到
,得到![]() ,
,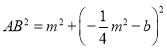 ,由
,由![]() 得到
得到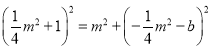 ,整理得
,整理得![]() ,故当
,故当![]() ,等式恒成立,故可得到B点坐标;
,等式恒成立,故可得到B点坐标;
(3)由(2)得![]() 永远成立,故
永远成立,故![]() ,故当点
,故当点![]() 在同一条直线上时,
在同一条直线上时, ![]() 的值最小,再根据P点的纵坐标即可求解.
的值最小,再根据P点的纵坐标即可求解.
解:![]()
![]() 抛物线
抛物线![]() 经过点
经过点![]()
![]()
![]()
![]() 抛物线解析式
抛物线解析式![]() ;
;
![]() 在抛物线对称轴上存在一定点
在抛物线对称轴上存在一定点![]() ,使得
,使得![]() 永远成立.
永远成立.
理由:设点![]() 坐标为
坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
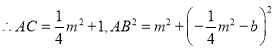
![]()
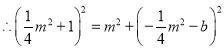
整理,得![]()
当![]() 时,
时,![]() ,
,![]() 恒成立
恒成立
![]() 点
点![]() 坐标为
坐标为![]() ;
;
![]() 由
由![]() 得
得![]() 永远成立,
永远成立,
![]()
![]() 当点
当点![]() 在同一条直线上时,
在同一条直线上时,
即![]() 时,
时,![]() 的值最小.
的值最小.
![]() 点
点![]() 坐标为
坐标为![]() 点纵坐标是
点纵坐标是![]() ,
,
![]() ,
,
![]() 的最小值是
的最小值是![]() .
.

练习册系列答案
相关题目