Question

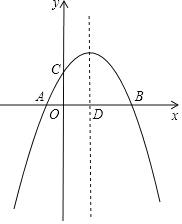
【题目】已知抛物线．

（1）用配方法求它的顶点坐标、对称轴；

（2）当的值在什么范围内时，随的增大而增大？当的值在什么范围内时，随的增大而减小？

（3）当的值在什么范围内时，抛物线在轴上方？

Answer 1

【答案】（1）顶点坐标是，对称轴是直线；（2）当时，随的增大而增大；当时，随的增大而减小；（3）当时，抛物线在轴上方．

【解析】

（1）根据配方法的要求把一般式转化为顶点式，根据顶点式的坐标特点，写出顶点坐标及对称轴；

（2）结合对称轴及开口方向确定抛物线的增减性；

（3）结合抛物线与x轴的交点坐标来确定抛物线位于x轴上方时，自变量的取值范围．

解：（1），

则顶点坐标是

对称轴是直线．

（2）∵a=且对称轴为直线

∴当时，随的增大而增大；

当时，随的增大而减小．

（3）令，则，

解得，，

，

抛物线开口向下，

当时，抛物线在轴上方．