Question

【题目】抛物线的图像与轴的一个交点为，另一交点为，与轴交于点，对称轴是直线．

（1）求该二次函数的表达式及顶点坐标；

（2）画出此二次函数的大致图象；利用图象回答：当取何值时，？

（3）若点在抛物线的图像上，且点到轴距离小于3，则的取值范围为 ；

Answer 1

【答案】（1），；（2）见解析，或；（3）

【解析】

（1）根据图像对称轴是直线，得到，再将， 代入解析式，得到关于a、b、c的方程组，即可求得系数，得到解析式，再求出顶点坐标即可；

（2）根据特定点画出二次函数的大致图象，根据二次函数与不等式的关系，即可得到对应的x的取值范围．

（3）求出当时，当时，y的值，即可求出的取值范围．

（1）因为图像对称轴是直线，所以，

将， 代入解析式，得：由题知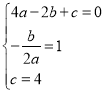，解得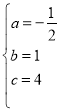，所以解析式为：；

当时，，所以顶点坐标．

（2）二次函数的大致图象：

当或，．

（3）当时，得，当时，得，

所以y取值范围为 ,即的取值范围为．