题目内容
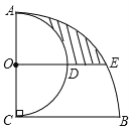
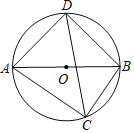
【题目】如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 分别在两个半圆上(不与点
分别在两个半圆上(不与点![]() 重合),
重合),![]() 的长分别是关于
的长分别是关于![]() 的方程
的方程![]()
![]() 的两个实数根.
的两个实数根.
(1)![]() 的值为_____;
的值为_____;
(2)连接![]() 三者之间的等量关系为_____.
三者之间的等量关系为_____.
【答案】![]()
![]() .
.
【解析】
(1)由方程有实数根可得出![]() ≥0,化简得(m-5)2≤0,由偶次方的非负性即可求出m的值;
≥0,化简得(m-5)2≤0,由偶次方的非负性即可求出m的值;
(2)由(1)可得出AD=BD,将△ADC绕点D逆时针旋转90°后,得△BDE,根据旋转的性质以及圆内接四边形的性质,可得出点C、B、E三点共线且△CDE为等腰直角三角形,根据等腰直角三角形的性质即可得出AC+BC=![]() CD.
CD.
解:(1)∵AD、BD的长分别是关于x的方程![]() 的两个实数根,
的两个实数根,
∴b2-4ac≥0,即(-10![]() )2-4×1×
)2-4×1×![]() (m2-10m+225)≥0,
(m2-10m+225)≥0,
化简整理,得:m2-10m+25≤0,即(m-5)2≤0.
又∵(m-5)2≥0,
∴m=5.
故答案为:5;
(2)由(1)得,当m=5时,b2-4ac=0,∴AD=BD.
∵AB是⊙O的直径,∴∠ACB=∠ADB=90°.
将△ADC绕点D逆时针旋转90°后,得△BDE,如图所示.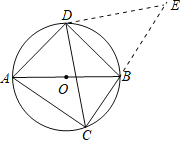
∴△ADC≌△BDE,
∴∠DAC=∠DBE,CD=ED,∠ADC=∠BDE.
∵∠DAC+∠DBC=180°,
∴∠DBE+∠DBC=180°,
∴点C、B、E三点共线.
∵∠ADC+∠CDB=90°,
∴∠CDE=∠CDB+∠BDE=90°.
又∵CD=ED,
∴△CDE为等腰直角三角形.
∴CE=![]() CD,
CD,
即AC+BC=![]() CD.
CD.
故答案为:AC+BC=![]() CD.
CD.

练习册系列答案
相关题目