Question

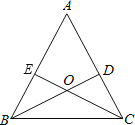
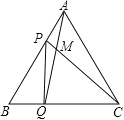
【题目】如图，点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点（其中P、Q不与端点重合），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ、CP交于点M，则在P、Q运动的过程中，下列结论：（1）BP=CM；（2）△ABQ≌△CAP；（3）∠CMQ的度数始终等于60°；（4）当第秒或第秒时，△PBQ为直角三角形．其中正确的结论有（ ）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】C

【解析】试题分析：易证△ABQ≌△CAP，可得∠AQB=∠CPA，即可求得∠AMP=∠B=60°，易证∠CQM≠60°，可得CQ≠CM，根据t的值易求BP，BQ的长，即可求得PQ的长，即可解题． ∵△ABC是等边三角形，

∴AB=BC=AC，∠BAC=∠B=∠ACB=60°， 根据题意得：AP=BQ， 在△ABQ和△CAP中，

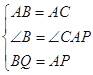， ∴△ABQ≌△CAP（SAS），（2）正确； ∴∠AQB=∠CPA，

∵∠BAQ+∠APC+∠AMP=180°，∠BAQ+∠B+∠AQB=180°， ∴∠AMP=∠B=60°，

∴∠QMC=60°，（3）正确； ∵∠QMC=60°，∠QCM≠60°， ∴∠CQM≠60°， ∴CQ≠CM，

∵BP=CQ， ∴CM≠BP，（1）错误； 当t=时，BQ=，BP=4﹣=，

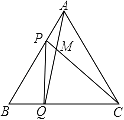
∵PQ2=BP2+BQ2﹣2BPBQcos60°， ∴PQ=， ∴△PBQ为直角三角形，

同理t=时，△PBQ为直角三角形仍然成立，（4）正确；