题目内容
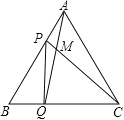
【题目】在Rt△ABC中，∠ACB=90°，∠A=30°，点D是AB的中点，DE⊥BC，垂足为点E，连接CD．
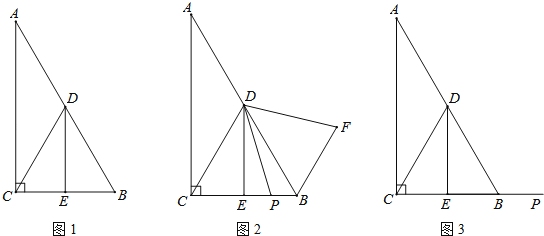
（1）如图1，DE与BC的数量关系是 ；
（2）如图2，若P是线段CB上一动点（点P不与点B、C重合），连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，连接BF，请猜想DE、BF、BP三者之间的数量关系，并证明你的结论；
（3）若点P是线段CB延长线上一动点，按照（2）中的作法，请在图3中补全图形，并直接写出DE、BF、BP三者之间的数量关系．
【答案】（1）DE=
BC（2）BF+BP=
DE．理由见解析（3）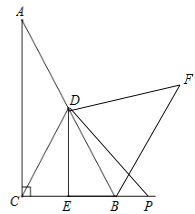
，BF﹣BP=
DE
【解析】
试题分析：（1）由∠ACB=90°，∠A=30°得到∠B=60°，根据直角三角形斜边上中线性质得到DB=DC，则可判断△DCB为等边三角形，由于DE⊥BC，DE=
BC；
（2）根据旋转的性质得到∠PDF=60°，DP=DF，易得∠CDP=∠BDF，则可根据“SAS”可判断△DCP≌△DBF，则CP=BF，利用CP=BC﹣BP，DE=BC可得到BF+BP=DE；
（3）与（2）的证明方法一样得到△DCP≌△DBF得到CP=BF，而CP=BC+BP，则BF﹣BP=BC，所以BF﹣BP=DE．
解：（1）∵∠ACB=90°，∠A=30°，
∴∠B=60°，
∵点D是AB的中点，
∴DB=DC，
∴△DCB为等边三角形，
∵DE⊥BC，
∴DE=BC；
故答案为DE=BC．
（2）BF+BP=DE．理由如下：
∵线段DP绕点D逆时针旋转60°，得到线段DF，
∴∠PDF=60°，DP=DF，
而∠CDB=60°，
∴∠CDB﹣∠PDB=∠PDF﹣∠PDB，
∴∠CDP=∠BDF，
在△DCP和△DBF中
，
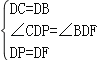∴△DCP≌△DBF（SAS），
∴CP=BF，
而CP=BC﹣BP，
∴BF+BP=BC，
∵DE=BC，
∴BC=DE，
∴BF+BP=DE；
（3）如图，
与（2）一样可证明△DCP≌△DBF，
∴CP=BF，
而CP=BC+BP，
∴BF﹣BP=BC，
∴BF﹣BP=DE．
