题目内容
如图,点A1,A2,A3,A4,…,An在射线OA上,点B1,B2,B3,…,Bn―1在射线OB上,且A1B1∥A2B2∥A3B3∥…∥An―1Bn―1,A2B1∥A3B2∥A4B3∥…∥AnBn―1,△A1A2B1,△A2A3B2,…,△An―1AnBn―1为阴影三角形,若△A2B1B2,△A3B2B3的面积分别为1、4,则△A1A2B1的面积为__________;面积小于2011的阴影三角形共有__________个.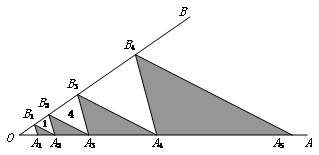

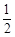 ;6
;6解:因为A1B1∥A2B2∥A3B3∥…∥An―1Bn―1,A2B1∥A3B2∥A4B3∥…∥AnBn―1,△A1A2B1,△A2A3B2,…,△An―1AnBn―1为阴影三角形,若△A2B1B2,△A3B2B3的面积分别为1、4,则△A2B1B2,△A3B2B3的相似比为1:2,则可得△A1A2B1的面积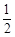 ,以后的每个阴影部分的三角形的面积构成了相似边的比为1:2:4:8:16:32… ,这样可知第六个三角形的面积为210=1024,第7个三角形的面积为212=4084则大于2011,故有6个三角形。
,以后的每个阴影部分的三角形的面积构成了相似边的比为1:2:4:8:16:32… ,这样可知第六个三角形的面积为210=1024,第7个三角形的面积为212=4084则大于2011,故有6个三角形。
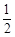 ,以后的每个阴影部分的三角形的面积构成了相似边的比为1:2:4:8:16:32… ,这样可知第六个三角形的面积为210=1024,第7个三角形的面积为212=4084则大于2011,故有6个三角形。
,以后的每个阴影部分的三角形的面积构成了相似边的比为1:2:4:8:16:32… ,这样可知第六个三角形的面积为210=1024,第7个三角形的面积为212=4084则大于2011,故有6个三角形。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
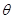 (0°<
(0°<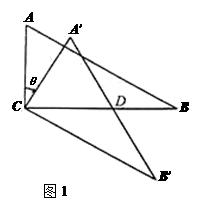
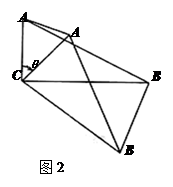
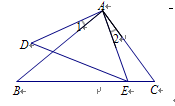
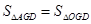 ;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有 ( ▲ )
;④四边形AEFG是菱形;⑤BE=2OG.其中正确的结论有 ( ▲ )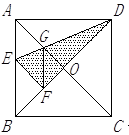

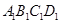 的面积是多少平方米?
的面积是多少平方米?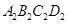 做一个纸箱比方案1更优,你认为呢?请说明理由.
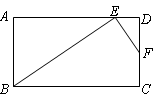
做一个纸箱比方案1更优,你认为呢?请说明理由.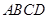 中,点
中,点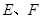 分别在边
分别在边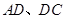 上,
上,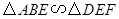
 ,求
,求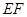 的长
的长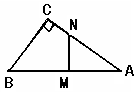
 cm
cm cm
cm