题目内容
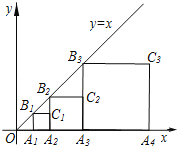
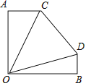
【题目】已知如图![]() ,在以
,在以![]() 为原点的平面直角坐标系中,抛物线
为原点的平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,直线
,直线![]() 过点
过点![]() 且平行于
且平行于![]() 轴,
轴,![]() ,
,
![]() 求抛物线对应的二次函数的解析式;
求抛物线对应的二次函数的解析式;
![]() 若
若![]() 为抛物线
为抛物线![]() 上一动点,是否存在直线
上一动点,是否存在直线![]() 使得点
使得点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长恒相等?若存在,求出此时
的长恒相等?若存在,求出此时![]() 的值;
的值;
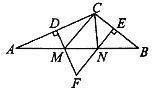
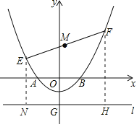
![]() 如图
如图![]() ,若
,若![]() 、
、![]() 为上述抛物线上的两个动点,且
为上述抛物线上的两个动点,且![]() ,线段
,线段![]() 的中点为
的中点为![]() ,求点
,求点![]() 纵坐标的最小值.
纵坐标的最小值.

【答案】(1)![]() ;(2)见解析;(3)2.
;(2)见解析;(3)2.
【解析】
(1)根据点C坐标,可得c=-1,然后根据AO=2CO,可得出点A坐标,将点A坐标代入求出b值,即可得出函数解析式;
(2)假设存在直线l使得点D到直线l的距离与OD的长恒相等,设出点D坐标,分别求出OD和点D到直线l的距离,然后列出等式求出t的值;
(3)作EN⊥直线l于点G,FH⊥直线l于点H,设出点E、F坐标,表示出点M的纵坐标,根据(2)中得出的结果,代入结果求出M纵坐标的最小值.
![]() ∵
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴点![]() 坐标为
坐标为![]() ,
,
代入得:![]() ,
,
解得:![]() ,
,
∴解析式为:![]() ;
;
![]() 假设存在直线
假设存在直线![]() 使得点
使得点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长恒相等,
的长恒相等,
设![]() ,
,
则![]() ,
,
点![]() 到直线
到直线![]() 的距离:
的距离:![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
故当![]() 时,直线
时,直线![]() 使得点
使得点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长恒相等;
的长恒相等;
![]() 作
作![]() 直线
直线![]() 于点
于点![]() ,
,![]() 直线
直线![]() 于点
于点![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∵![]() 为
为![]() 中点,
中点,
∴![]() 纵坐标为:
纵坐标为:![]() ,
,
由![]() 得:
得:![]() ,
,![]() ,
,
∴![]() ,
,
要使![]() 纵坐标最小,即
纵坐标最小,即![]() 最小,
最小,
当![]() 过点
过点![]() 时,
时,![]() 最小,最小值为
最小,最小值为![]() ,
,
∴![]() 纵坐标最小值为
纵坐标最小值为![]() .
.

【题目】某学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制作了不完整的统计图表.
学生借阅图书的次数统计表
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 6 | 15 | a | 12 | 9 |
学生借阅图书的次数扇形统计图

请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)该样本数据的中位数是 次,众数是 次;
(3)请计算扇形统计图中“3次”所对应的扇形圆心角的度数;
(4)若该校共有2400名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.