题目内容
【题目】如图,在![]() 中,
中,![]() 、
、![]() 分别垂直平分
分别垂直平分![]() 和
和![]() ,交
,交![]() 于
于![]() 、
、![]() 两点,
两点,![]() 与
与![]() 相交于点
相交于点![]() .
.
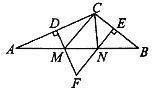
(1)若![]() 的周长为15 cm,求
的周长为15 cm,求![]() 的长.
的长.
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1) 15cm ; (2)40°.
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AM=CM,BN=CN,再求得△CMN的周长=AB,由此求得AB的长;(2)根据三角形的内角和定理求得∠MNF+∠NMF的度数,再求出∠A+∠B的度数,根据等边对等角可得∠A=∠ACM,∠B=∠BCN,利用三角形的内角和定理列式计算即可求解.
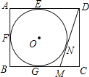
(1)∵DM、EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB,
∵△CMN的周长为15cm,
∴AB=15cm;
(2)∵∠MFN=70°,
∴∠MNF+∠NMF=180°-70°=110°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=110°,
∴∠A+∠B=90°-∠AMD+90°-∠BNE=180°-110°=70°,
∵AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°-2(∠A+∠B)=180°-2×70°=40°.

练习册系列答案
相关题目