题目内容
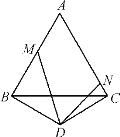
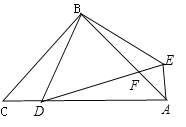
【题目】如图,已知:在△ABC中,∠ABC=90°,AB=BC=2,AC=2![]() ,D是边AC上一点(D与A、C不重合),过点A作AE垂直AC,求满足AE=CD,联结DE交边AB于点F.
,D是边AC上一点(D与A、C不重合),过点A作AE垂直AC,求满足AE=CD,联结DE交边AB于点F.
(1)试判断△DBE的形状,并证明你的结论.
(2)当点D在边AC上运动时,四边形ADBE的面积是否发生变化?若不变,求出四边形ADBE的面积;若改变,请说明理由.
(3)当△BDF是等腰三角形时,请直接写出AD的长.

【答案】(1)△DBE是等腰直角三角形,证明见解析;(2)不变;2;(3)![]() 或2.
或2.
【解析】
(1)根据在△ABC中,∠ABC=90°,AB=BC=2可得出∠CAB=∠ACB=45°,再由AE⊥AC可得出∠EAC=90°,故可得出∠BAE=45°,由SAS定理可得出△CBD≌△ABE,故可得出BD=BE,由此可得出结论;
(2)根据(1)中△CBD≌△ABE可知四边形ADBE的面积不变,再由三角形的面积公式即可得出结论;
(3)分两种情况分别讨论即可求得.
(1)△DBE是等腰直角三角形.
理由:∵∠ABC=90°,AB=BC=2,
∴∠CAB=∠ACB=45°.
∵AE⊥AC,
∴∠EAC=90°,
∴∠BAE=45°.
在△CBD与△ABE中,
∵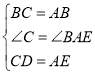 ,
,
∴△CBD≌△ABE(SAS),
∴BD=BE,∠CBD=∠ABE,
∵∠CBD+∠ABD=90°,
∴∠ABE+∠ABD=90°,
即∠BDE=90°,
即△DBE是等腰直角三角形;
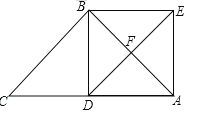
(2)不变.
∵由(1)知△CBD≌△ABE,
∴S四边形ADBE=S△ABC=![]() ×2×2=2;
×2×2=2;
(3)当BF=DF时,则∠BDE=∠FBD,
∵△DBE是等腰直角三角形,
∴∠BDE=45°,
∴∠FBD=45°
∴∠CBD=45°,
∴∠CBD=∠ABD,
∴AD=CD,
∴AD=![]() AC,
AC,
∵AB=BC=2,
∴AC=2![]()
∴AD=![]() ;
;
当BD=DF时,
∵△ABC是等腰直角三角形,△BDE是等腰直角三角形,
∴∠C=∠CAB=45°,∠BDE=∠BED=45°,
∴∠C=∠BDE,
∵∠ADB=∠C+∠CBD=∠BDE+∠FDA,
∴∠CDB=∠ADF,
在△BCD和△DAF中
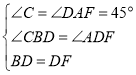
∴△BCD≌△DAF(AAS),
∴AD=BC=2.
∴当△BDF是等腰三角形时,AD的长为![]() 或2.
或2.

 阅读快车系列答案
阅读快车系列答案