题目内容
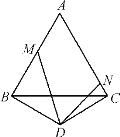
【题目】如图,CD平分∠ACB,点D是AB的中点,AE∥DC,AE交BC的延长线于点E,且∠ACE=60°,BC=8.求△ACE的周长.

【答案】24
【解析】
由题意可得∠E=∠ACE=60°,进而可得△ACE是等边三角形,延长CD到点F,使DF=CD,连接AF,利用SAS可证△ADF≌△BDC,可得∠F=∠BCD=60°,AF=BC,进一步可得△ACF是等边三角形,进而可得AC=BC,问题即得解决.
解:∵∠ACE=60°,∴∠ACB=120°,
又CD平分∠ACB,∴∠BCD=60°,
∵AE∥DC,
∴∠E=∠BCD=60°,
∴△ACE是等边三角形,
延长CD到点F,使DF=CD,连接AF,如图,
∵点D是AB的中点,∴DA=DB,
又∵∠ADF=∠BDC,
∴△ADF≌△BDC(SAS),
∴∠F=∠BCD=60°,AF=BC,
∵∠ACD=60°,
∴△ACF是等边三角形,
∴AC=AF,
∴AC=BC=8,
∴△ACE的周长为24.

练习册系列答案
相关题目