题目内容
如图，在Rt△ABC中，∠ABO=90°，OB=4，AB=8，且反比例函数
在第一象限内的图象分别交OA、AB于点C和点D，连结OD，若
，
(1)求反比例函数解析式；
(2)求C点坐标．
（1）
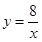；（2）（2，4）．
解析试题分析：(1)由，且OB=4，可求BD的长，因此D点坐标可求，从而确定反比例函数解析式.
（2）过点C作CE⊥OB于点E．在
中，利用锐角三角函数可求出CE和OE的长，从而求出C点坐标．
试题解析：（1）设D（x，y），
则有OB=x，BD=y．
由 ，得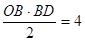
，
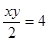， xy=8．
由可得，k=xy，∴k=8，
∴
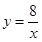
（2）过点C作CE⊥OB于点E．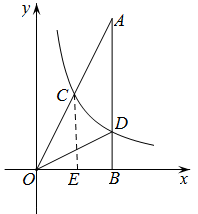
在中，
，
，
，
∴tan∠AOB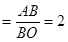
，
∴
，CE=2EO，
设C点坐标为（a，2a），
把点C（a，2a）代入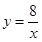中，得
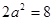，解得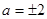
，
∵点C在第一象限，∴a>0，取a=2．
∴C点坐标为（2，4）．
考点: 反比例函数综合题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
（k＞0）上，则a、b、c的大小关系为 （用“＜”将a、b、c连接起来）．
的图象和矩形ABCD在第二象限，AD平行于x轴，且AB=2，AD=4，点C的坐标为（-2，4）．
的x取值范围．
（k为常数，k≠1）.
（x＞0）图象上任意一点，以P为圆心，PO为半径的圆与坐标轴分别交于点A、B．
的图象与反比例函数
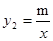的图象的两个交点是A（－2，－4），C（4，n），与y轴交于点B，与x轴交于点D．
的图象与一次函数y=kx+b的图象相交于两点A（m，3）和B（﹣3，n）．
在反比例函数
的图象上,它关于
轴的对称点在一次函数
的图象上,求此反比例函数的解析式．
（k≠0）和一次函数y=x﹣6．