题目内容
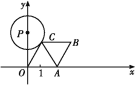
【题目】如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O,A为顶点作菱形OABC,使B,C点都在第一象限内,且AO=AC,又以P(0,4![]() )为圆心,PC为半径的圆恰好与OC所在的直线相切,则t等于( )
)为圆心,PC为半径的圆恰好与OC所在的直线相切,则t等于( )
A. 2![]() -1 B. 2
-1 B. 2![]() +1 C. 5 D. 7
+1 C. 5 D. 7
【答案】C
【解析】
如下图,连接CP,由已知易得OC=OA=AC=1+t,OP=![]() ,∠PCO=90°,由此易得∠AOC=60°,∠POC=30°,这样在Rt△OPC中,即可解得OC=6,结合OC=1+t即可t=5.
,∠PCO=90°,由此易得∠AOC=60°,∠POC=30°,这样在Rt△OPC中,即可解得OC=6,结合OC=1+t即可t=5.
如下图,连接PC,
∵已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,且经过t秒,
∴OA=1+t,
∵四边形OABC是菱形,
∴OC=OA=1+t,
∵☉P恰好与OC所在的直线相切,
∴PC⊥OC,
∴∠OCP=90°,
∵AC=AO=OC,
∴∠AOC=60°,∠COP=30°,
∴在Rt△OPC中,PC=![]() OP=2
OP=2![]() ,
,
∴OC=6,
∴1+t=6,解得:t=5.
故选C.

练习册系列答案
相关题目