题目内容
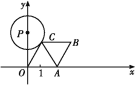
【题目】如图,∠BCD=90°,且BC=DC,直线PQ经过点D.设∠PDC=α(45°<α<135°),BA⊥PQ于点A,将射线CA绕点C按逆时针方向旋转90°,与直线PQ交于点E.
(1)当α=125°时,∠ABC= °;
(2)求证:AC=CE;
(3)若△ABC的外心在其内部,直接写出α的取值范围.

【答案】(1)125;(2)详见解析;(3)45°<α<90°.
【解析】
(1)利用四边形内角和等于360度得:∠B+∠ADC=180°,而∠ADC+∠EDC=180°,即可求解;
(2)证明△ABC≌△EDC(AAS)即可求解;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,∠ABC=α>90°时,△ABC的外心在其外部,即可求解.
解:(1)在四边形BADC中,∠B+∠ADC=360°﹣∠BAD﹣∠DCB=180°,
而∠ADC+∠EDC=180°,
∴∠ABC=∠PDC=α=125°,
故答案为125;
(2)∠ECD+∠DCA=90°,∠DCA+∠ACB=90°,
∴∠ACB=∠ECD,
又BC=DC,由(1)知:∠ABC=∠PDC,
∴△ABC≌△EDC(AAS),
∴AC=CE;
(3)当∠ABC=α=90°时,△ABC的外心在其直角边上,
∠ABC=α>90°时,△ABC的外心在其外部,
而45°<α<135°,
故:45°<α<90°.

【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .