��Ŀ����
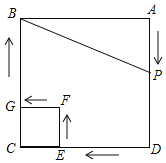
����Ŀ����ͼ���߳�Ϊ4�Ĵ�������ABCD����һ���߳�Ϊ1��С������CEFG������P��ÿ��1cm���ٶȴӵ�A��������A��D��E��F��G��B��·���ƶ���εı������˶�����Bֹͣ��������A�͵�B��������ABP�����ΪS����P���˶�ʱ��Ϊt��
��1��Сӱͨ������Ĺ۲�������ó���һ����ȷ�Ľ��ۣ�����P���߶�DE���˶�ʱ����������ͬ�ȸ�����������˵���P���߶�DE���˶�ʱ��ABP�����Sʼ�ղ������仯��
�ʣ��ڵ�P���˶������У����������Ƶ������������ڣ���˵��P��λ�ã��������ڣ���˵�����ɣ�
��2���ڵ�P���˶���������ABP�����S�Ƿ�������ֵ�������ڣ���������������������ڣ���˵�����ɣ�
��3����д��S��t֮��Ĺ�ϵʽ��

���𰸡���1���ڵ�P���˶������У����������Ƶ�������P���߶�GF���˶�ʱ����������ͬ�ȸ�����������P���߶�GF���˶�ʱ����ABP�����Sʼ�ղ������仯����2��8����3���ٵ���P��AD��ʱ��S =2t��0��t��4����
�ڵ���P��DE��ʱ��S=8��4��t��7����
�۵���P��EF��ʱ��S=22-2t��7��t��8����
�ܵ���P��GF��ʱ��S=6��8��t��9����
�ݵ���P��GB��ʱ��S=24-2t��9��t��12����
��������
��1������GF��AB���ɵõ���P���߶�GF���˶�ʱ����������ͬ�ȸ�������������P���߶�GF���˶�ʱ����ABP�����Sʼ�ղ������仯��
��2������P���߶�DE���˶�ʱ��AB���ϵĸ�Ϊ4���ݴ˿ɵ���ABP�����S���ֵΪ��![]() AB��AD=
AB��AD=![]() ��4��4=8��
��4��4=8��
��3����5������������ۣ��ٵ���P��AD��ʱ���ڵ���P��DE��ʱ���۵���P��EF��ʱ���ܵ���P��GF��ʱ���ݵ���P��GB��ʱ���ֱ������ABP��������㷽�����ó�S��t֮��Ĺ�ϵʽ��
��1���ڵ�P���˶������У����������Ƶ�����
�ߡ�ABG+��BGF=180����
��GF��AB��
�൱��P���߶�GF���˶�ʱ����������ͬ�ȸ���������
�൱��P���߶�GF���˶�ʱ����ABP�����Sʼ�ղ������仯��
��2���ߡ�ABP�У�AB�ij����䣬
�൱AB���ϵĸ����ʱ����ABP�����S�������ֵ��
�ʵ���P���߶�DE���˶�ʱ��AB���ϵĸ�Ϊ4��
���ABP�����S���ֵΪ��![]() AB��AD=
AB��AD=![]() ��4��4=8��
��4��4=8��
��3����5�������
�ٵ���P��AD��ʱ��S=![]() ��4��t=2t��0��t��4����
��4��t=2t��0��t��4����
�ڵ���P��DE��ʱ��S=![]() ��4��4=8��4��t��7����
��4��4=8��4��t��7����
�۵���P��EF��ʱ��S=![]() ��4��[4-��t-7��]=2��11-t��=22-2t��7��t��8����
��4��[4-��t-7��]=2��11-t��=22-2t��7��t��8����
�ܵ���P��GF��ʱ��S=![]() ��4��3=6��8��t��9����
��4��3=6��8��t��9����
�ݵ���P��GB��ʱ��S=![]() ��4��[4-��t-8��]=2��12-t��=24-2t��9��t��12����
��4��[4-��t-8��]=2��12-t��=24-2t��9��t��12����