Question

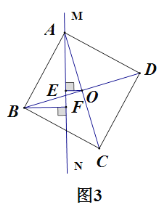
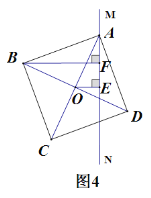
【题目】如图，，分别是以，为斜边的直角三角形，，是等边三角形.

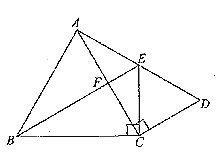
（1）求证：；

（2）若，求的长.

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）根据等边三角形CDE的性质、等量代换求得∠3=∠1=60°；然后由全等三角形Rt△BCE和Rt△ACD推知对应边BC=AC, ；从而判定△ABC是等边三角形，再利用等边三角形的性质即可得出答案．

（2）先根据直角三角形中30°角所对的直角边等于斜边的一半的性质得出EF长，再根据得出的长

（1）证明：∵△CDE是等边三角形，
∴EC=CD，∠1=∠D=60°．
∵BE、AD都是斜边，

∴∠BCE=∠ACD=90°, ∠CAD=30°

在与中，

，

∴，

∴BC=AC． ∠CAD=∠CBE =30°
∵∠1+∠2=90°，∠3+∠2=90°，
∴∠3=∠1=60°．
∴△ABC是等边三角形．

∴∠ABC=60°

∴∠CAD=∠CBE =30°

∴.

（2）∵，

∴，

在Rt,∠CBE =30°

∴，

又∵∠ECF=90°-∠DCE =30°，

∴，

∴.