题目内容
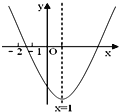
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:①b2﹣4ac>0 ②a>0 ③b>0 ④c>0 ⑤9a+3b+c<0,则其中结论正确的个数是( )
A、2个B、3个
C、4个D、5个
【答案】B
【解析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据抛物线与x轴交点及x=1时二次函数的值的情况进行推理,进而对所得结论进行判断.
解答:解:①根据图示知,二次函数与x轴有两个交点,所以△=b2-4ac>0;故①正确;
②根据图示知,该函数图象的开口向上,
∴a>0;
故②正确;
③又对称轴x=-![]() =1,
=1,
∴![]() <0,
<0,
∴b<0;
故本选项错误;
④该函数图象交于y轴的负半轴,
∴c<0;
故本选项错误;
⑤根据抛物线的对称轴方程可知:(-1,0)关于对称轴的对称点是(3,0);
当x=-1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故⑤正确.
所以①②⑤三项正确.
故选B.

练习册系列答案
相关题目
【题目】随机抽取某市一年(以365天计)中的30天的日平均气温状况统计如下:温度(![]() )
)
温度( | 10 | 14 | 18 | 22 | 26 | 30 | 32 |
天数 | 3 | 5 | 5 | 7 | 6 | 2 | 2 |
请根据上述数据回答下列问题:
(1)估计该城市年平均气温大约是多少?
(2)上表中的温度数据的中位数是_______众数是_________;
(3)计算该城市一年中约有几天的日平均气温为![]() ?
?