题目内容
【题目】已知△ABC中,AH⊥BC，垂足为H,若AB+BH=CH,∠ABH=80°,则∠BAC=_________ 。
【答案】60°或40°
【解析】
分锐角三角形和钝角三角形两种情况讨论：锐角三角形时，在CH上截取DH=BH，连接AD，即可得到△ABH≌△ADH，进而得到CD=AD，再由三角形外角的性质即可得出∠B的大小；钝角三角形时，直接由三角形外角的性质即可得出∠B的大小.
当△ABC为锐角三角形时，
在CH上截取DH=BH，连接AD，如图：
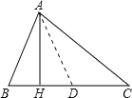
∵AH⊥BC，
∴∠AHB=∠AHD=90°，
在△ABH≌△ADH中，
∵
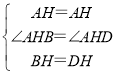
∴△ABH≌△ADH(SAS)，
∴AD=AB，∠ABH=∠ADB=80°，∠BAH=∠DAH
，
∵AB+BH= CH，HD+CD=CH
∴AD=CD
∴∠C=∠DAC=
40
，
∴∠
．
当△ABC为钝角三角形时，
如图：
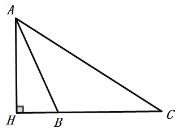
∵AB+BH= CH，BC+ BH =CH
∴AB=CB
∴∠BAC=∠C=
40，
故答案为：60°或40°
练习册系列答案
相关题目
