题目内容
【题目】正方形ABCD的边AB在直线MN上,O是AC、BD的交点,过O作OE⊥MN于点E.
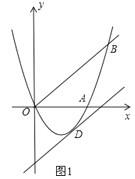
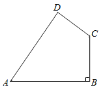
(1)如图1,线段AB与OE之间的数量关系为 .(请直接填结论)
(2)保证点A始终在直线MN上,正方形ABCD绕点A旋转![]() (0<
(0<![]() <90°),过点B作BF⊥MN于点F.
<90°),过点B作BF⊥MN于点F.
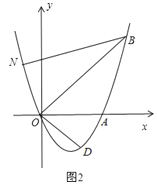
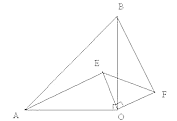
① 如图2,当点O、B两点均在直线MN右侧时,试猜想线段AF、BF与OE之间存在怎样的数量关系?请说明理由.
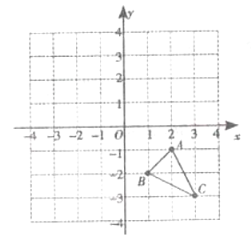
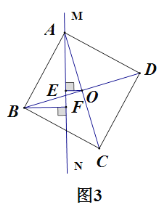
② 如图3,当点O、B两点分别在直线MN两侧时,此时①中结论是否依然成立呢?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.


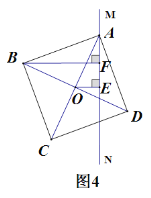
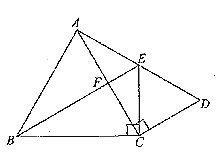
③ 当正方形ABCD绕点A旋转到如图4的位置时,线段AF、BF与OE之间的数量关系为 .(请直接填结论)
【答案】(1)AB=2OE;(2)①AF+BF=2OE, ②AF-BF=2OE, ③BF-AF=2OE,详见解析.
【解析】
(1)过点B作BG⊥OE于G,可得四边形BGEF是矩形,根据矩形的对边相等可得EF=BG,BF=GE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBG,然后利用“角角边”证明△AOE和△OBG全等,根据全等三角形对应边相等可得OG=AE,OE=BG,再根据AF-EF=AE,整理即可得证;
(2)图2,过点B作BG⊥OE交OE的延长线于G,可得四边形BGEF是矩形,根据矩形的对边相等可得EF=BG,BF=GE,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠OBG,然后利用“角角边”证明△AOE和△OBG全等,根据全等三角形对应边相等可得OG=AE,OE=BG,再根据AF-EF=AE,整理即可得证;
(3)图3,作OG⊥BF于G,可得四边形EFGO是矩形,根据矩形的对边相等可得EF=GO,GF=EO,根据正方形的对角线相等且互相垂直平分可得OA=OB,∠AOB=90°,再根据同角的余角相等求出∠AOE=∠BOG,然后利用“角角边”证明△AOE和△BOG全等,根据全等三角形对应边相等可得OG=OE,AE=BG,再根据BF-BG=GF,整理即可得证.
(1)AB=2OE
(2)①AF+BF=2OE,
证明:过点B作BH⊥OE于点H∴∠BHE=∠BHO=90°∵OE⊥MN,BF⊥MN
∴∠BFE=∠OEF=90°∴四边形EFBH为矩形∴BF=EH,EF=BH
∵四边形ABCD为正方形∴OA=OB,∠AOB=90°∴∠AOE+∠HOB=∠OBH+∠HOB=90°
∴∠AOE=∠OBH∴△AEO≌△OHB(AAS)∴AE=OH,OE=BH
∴AF+BF=AE+EF+BF=OH+BH+EH=OE+OE=2OE.
②AF-BF=2OE,
证明:延长OE,过点B作BH⊥OE于点H
∴∠EHB=90°
∵OE⊥MN,BF⊥MN
∴∠AEO=∠HEF=∠BFE=90°
∴四边形HBFE为矩形∴BF=HE,EF=BH
∵四边形ABCD是正方形
∴OA=OB,∠AOB=90°∴∠AOE+∠BOH=∠OBH+∠BOH
∴∠AOE=∠OBH∴△AOE≌△OBH(AAS)
∴AE=OH,OE=BH∴AF-BF
=AE+EF-HE=OH-HE+OE=OE+OE=2OE

③BF-AF=2OE

【题目】随机抽取某市一年(以365天计)中的30天的日平均气温状况统计如下:温度(![]() )
)
温度( | 10 | 14 | 18 | 22 | 26 | 30 | 32 |
天数 | 3 | 5 | 5 | 7 | 6 | 2 | 2 |
请根据上述数据回答下列问题:
(1)估计该城市年平均气温大约是多少?
(2)上表中的温度数据的中位数是_______众数是_________;
(3)计算该城市一年中约有几天的日平均气温为![]() ?
?