题目内容
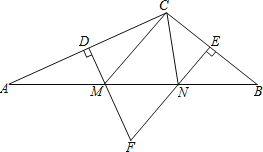
【题目】如图,在![]() 中,
中,![]() 分别垂直平分
分别垂直平分![]() 和
和![]() ,交
,交![]() 于
于![]() 两点,
两点,![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)若![]() =21cm,则
=21cm,则![]() 的周长= ;(第一问直接写答案)
的周长= ;(第一问直接写答案)
(2)若![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)21cm;(2)20°
【解析】
(1)根据线段的垂直平分线的性质,可知,AM=CM,BN=CN,然后,即可求出![]() 的周长;
的周长;
(2)根据三角形的内角和定理,求出∠MNF+∠NMF,进而求出∠A+∠B,根据等腰三角形的性质,可知,∠A=∠ACM,∠B=∠BCN,最后,利用三角形内角和定理,即可求解.
(1)∵![]() 分别垂直平分
分别垂直平分![]() 和
和![]() ,
,
∴AM=CM,BN=CN,
∴![]() 的周长=CM+CN+MN=AM+BN+MN=AB=21cm;
的周长=CM+CN+MN=AM+BN+MN=AB=21cm;
(2)∵![]() ,
,
∴∠MNF+∠NMF=180°-∠MFN=180°-80°=100°,
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠MNF+∠NMF=100°,
∴∠A+∠B=90°-∠AMD+90°-∠BNE=180°-100°=80°,
由(1)可知,AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°-2(∠A+∠B)=180°-2×80°=20°.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目