题目内容
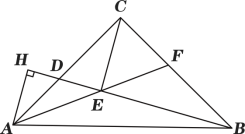
【题目】如图，在△ABC中，∠ACB=90°，AC=BC，点D为边AC上一点，连接BD，作AH⊥BD的延长线于点H，过点C作CE//AH与BD交与点E，连结AE并延长与BC交于点F．现有如下4个结论：①∠HAD=∠CBD；②△ADE∽△BFE；③CE·AH=HD·BE；④若D为AC中点，则
，其中正确结论有( )个．
A.1个B.2个C.3个D.4个
【答案】B
【解析】
在
与
中，利用三角形的内角和定理判断①，由相似三角形逆推得到与已知条件互相矛盾的结论判断②，利用已知条件证明
判断③，利用相似三角形与平行线分线段成比例判断④．
解：
∠ACB=90°，AH⊥BD，
所以①正确．
在△ADE与△BFE中，若△ADE∽△BFE，
则
为
的中垂线，
与
相交，
所以②错误，
由
所以③正确，
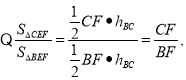
显然：
与
不平行，
所以
错误，故④错误．
故选B．
练习册系列答案
名校课堂系列答案
相关题目
