题目内容
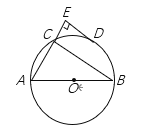
【题目】如图:点A(0,4),B(0,﹣6),C为x轴正半轴上一点,且满足∠ACB=45°,则( )
A.OC=12B.△ABC外接圆的半径等于![]()
C.∠BAC=60°D.△ABC外接圆的圆心在OC上
【答案】A
【解析】
构造含有90°圆心角的⊙P,则⊙P与x轴的交点即为所求的点C.根据△PBA为等腰直角三角形,可得OF=PE=5,根据勾股定理得:CF=7,进而得出OC.
设线段BA的中点为E,
∵点A(0,4),B(0,6),
∴AB=10,E(0,1).
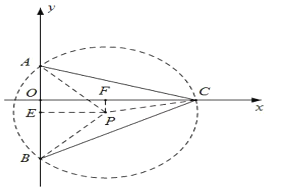
如图所示,过点E在第四象限作EP⊥BA,且EP=![]() AB=5,则
AB=5,则
易知△PBA为等腰直角三角形,∠BPA=90°,PA=PB=5![]() ;
;
以点P为圆心,PA(或PB)长为半径作⊙P,与y轴的正半轴交于点C,
∵∠BCA为⊙P的圆周角,
∴∠BCA=![]() ∠BPA=45°,即则点C即为所求.
∠BPA=45°,即则点C即为所求.
过点P作PF⊥x轴于点F,则OF=PE=5,PF=OE=1,
在Rt△PFC中,PF=1,PC=5![]() ,
,
由勾股定理得:CF=![]() =7,
=7,
∴OC=OF+CF=5+7=12,
故选:A.

【题目】为响应垃圾分类处理,改善生态环境,某小区将生活垃圾分成三类:厨余垃圾、可回收垃圾和其他垃圾,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为A,B,C
(1)小明将垃圾分装在三个袋中,任意投放,用画树状图或列表的方法求把三个袋子都放错位置的概率是多少?
(2)某学习小组为了了解居民生活垃圾分类投放的情况,现随机抽取了某天三类垃圾箱中总共100吨的生活垃圾,数据统计如表(单位:吨):
A | B | C | |
a | 40 | 10 | 10 |
b | 3 | 24 | 3 |
c | 2 | 2 | 6 |
调查发现,在“可回收垃圾”中塑料类垃圾占10%,每回收1吨塑料类垃圾可获得0.7吨二级原料,某城市每天大约产生200吨生活垃圾假设该城市每天处理投放正确的垃圾,每天大概可回收多少吨塑料类垃圾的二级原料?