题目内容
【题目】如图,已知AB、AC分别为⊙O的直径和弦,D为![]() 的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm, CE=2cm,下列结论:①. DE是⊙O的切线;②. 直径AB长为20cm;③. 弦AC长为15cm;④. C为
的中点,DE垂直于AC的延长线于E,连结BC,若DE=6cm, CE=2cm,下列结论:①. DE是⊙O的切线;②. 直径AB长为20cm;③. 弦AC长为15cm;④. C为![]() 的中点.一定正确的个数是( )
的中点.一定正确的个数是( )
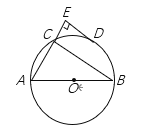
A.1B.2C.3D.4
【答案】B
【解析】
连接OD,OC,交BC于点F,可证明DE∥BC,可判断A;在△OCF中,由垂径定理结合勾股定理可求得圆的半径,可判断B;由垂径定理可求得BC的长,结合B可判断C;由弧相等可得弦相等可判断D.
解:连接OD,OC.
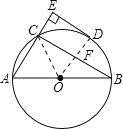
∵D是弧BC的中点,
∴OD⊥BC,
∵AB是直径,
∴∠ACB=90°,
∵DE垂直于AC的延长线于E,
∴BC∥DE,
∴OD⊥DE,
∴DE是圆的切线.故①正确;
∵OD⊥BC,DE⊥CE,OD⊥DE,
∴四边形DECF是矩形,
∴DF=CE=2cm,CF=DE=6cm,
∴BC=2CF=12cm,
设半径为rcm,则OF=(r-2)cm,
在Rt△OCF中,
由勾股定理可得OC2=OF2+CF2,
即r2=(r-2)2+62,
解得r=10cm,
∴AB=20cm,
故②正确;
在Rt△ABC中,BC=12cm,AB=20cm,
∴AC= ![]() =16(cm),
=16(cm),
故③不正确;
若C为弧AD的中点,则AC=CD,
在Rt△CDE中,CE=2cm,DE=6cm,由勾股定理可求得CD=2![]() cm≠AC,
cm≠AC,
故④不正确;
故选: B.

练习册系列答案
相关题目