题目内容
【题目】阅读材料，解决问题：
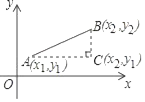
如图，为了求平面直角坐标系中任意两点A（x1，y1）、B（x2，y2）之间的距离，可以AB为斜边作Rt△ABC，则点C的坐标为C（x2，y1），于是AC＝|x1﹣x2|，BC＝|y1﹣y2|，根据勾股定理可得AB＝
，反之，可以将代数式的值看做平面内点（x1，y1）到点（x2，y2）的距离．
例如∵
=
=
，可将代数式看作平面内点（x，y）到点（﹣1，3）的距离
根据以上材料解决下列问题
（1）求平面内点M（2，﹣3）与点N（﹣1，3）之间的距离；
（2）求代数式
的最小值．
【答案】（1）3
（2）2
【解析】
（1）依据两点间的距离公式进行计算即可；
（2）先将原式变形，即可将原式可以看作点P（x，y）到点（3，4）和点（﹣5，2）的距离之和，求得AB的长，即可得到该代数式的最小值．
（1）MN＝
＝3；
（2）∵原式＝
＝
+
，
∴原式可以看作点P（x，y）到点（3，4）和点（﹣5，2）的距离之和，
∴当点P（x，y）在线段AB上时，原式有最小值，
∵AB＝
＝
，
∴原式的最小值为2．
练习册系列答案
相关题目
