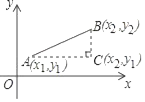
题目内容
【题目】如图1,折叠矩形纸片ABCD,具体操作:①点E为AD边上一点(不与点A,D重合),把△ABE沿BE所在的直线折叠,A点的对称点为F点;②过点E对折∠DEF,折痕EG所在的直线交DC于点G,D点的对称点为H点.
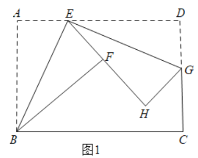
(1)求证:△ABE∽△DEG.
(2)若AB=3,BC=5
①点E在移动的过程中,求DG的最大值
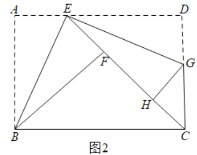
②如图2,若点C恰在直线EF上,连接DH,求线段DH的长.
【答案】(1)详见解析;(2)①![]() 时,
时,![]() 有最大值
有最大值![]() ;②
;②![]()
【解析】
(1)根据两角对应相等两三角形相似证明即可;
(2)①设AE=x,证明△ABE∽△DEG,推出![]() ,可以得到
,可以得到![]() ,利用二次函数的性质求解即可;
,利用二次函数的性质求解即可;
②如图2中,连接DH.解直角三角形求出AE,DE,DG,EG,由翻折的性质可知EG垂直平分线段DH,利用面积法可得![]() .
.
(1)由折叠可知![]() ,
,![]()
∵![]()
∴![]()
∵矩形![]()
∴![]()
∴![]()
∴![]()
(2)①设![]()
∵![]()

(2)①设![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,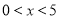
∴![]() 时,
时,![]() 有最大值
有最大值![]()
②由折叠可知![]() ,
,![]() ,
,![]()
![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵点![]() 在直线
在直线![]() 上
上
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴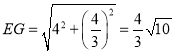
由折叠可知![]()
∴

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
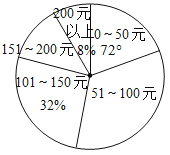
小学生10分钟应用题系列答案【题目】某社区踊跃为“抗击肺炎”捐款,根据捐款情况(捐款数为正数)制作以下统计图表,但工作人员不小心把墨水滴在统计表上,部分数据看不清楚.
(1)共有多少人捐款?
(2)如果捐款0~50元的人数在扇形统计图中所占的圆心角为72°,那么捐款51~100元的有多少人?
捐款 | 人数 |
0~50元 | |
51~100元 | |
101~150元 | |
151~200元 | 6 |
200元以上 | 4 |
【题目】某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
七年级 | a | 85 | b | S七年级2 |
八年级 | 85 | c | 100 | 160 |
(1)根据图示填空:a= ,b= ,c= ;
(2)结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?
(3)计算七年级代表队决赛成绩的方差S七年级2,并判断哪一个代表队选手成绩较为稳定.