题目内容
【题目】已知，如图，在R t△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于D．
（1）动手操作：利用尺规作，以AB边上一点O为圆心，过A，D两点作⊙O，与AB的另一个交点为E，与AC的另一个交点为F（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由。
（2）若∠BAC=60度，CD= 
，求线段BD、BE与劣弧DE所围成的图形面积．（结果保留根号和 
）
【答案】
（1）解：如图1；
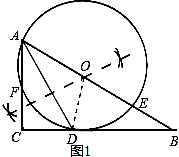
（2）解：（1）直线BC与⊙O的位置关系为相切．理由如下：
如图1，连接OD，
∵OA=OD，
∴∠OAD=∠ADO，
∵∠BAC的角平分线AD交BC边于D，
∴∠CAD=∠OAD，
∴∠CAD=∠ADO，
∴AC∥OD，
∵∠C=90°，
∴∠ODB=90°，
∴OD⊥BC，
即直线BC是⊙O的切线，
∴直线BC与⊙O的位置关系为相切；
（2）如图2，
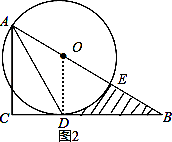
∵∠BAC的角平分线AD交BC于D，∠BAC=60°，∠C=90°，
∴∠CAD=∠DAB=30°，∠B=30°，
∴∠DAB=∠B=30°，
∴BD=AD．
∵在Rt△ADC中，∠C=90°，∠CAD=30°，CD= 
，
∴AD=2CD=2 ，AC= CD=3，
∴BD=2 ，AB=2AC=6．
设⊙O的半径为r，
在Rt△OBD中，OD2+BD2=OB2，
即r2+（2 ）2=（6﹣r）2，
解得r=2，OB=6﹣r=4，
∵∠ODB=90°，∠B=30°，
∴∠DOB=60°，
∴S扇形ODE= 
，
S△ODB= 
ODBD= ×2×2 =2 ，
∴线段BD、BE与劣弧DE所围成的图形面积为：S△ODB﹣S扇形ODE= 
．
【解析】（1）根据题意作线段AD的垂直平分线，交AB于点O，以O为圆心，OA为半径画圆。要证直线BC于圆相切，因此连接OD，去证明OD⊥BC。先根据角平分线的定义得出∠CAD=∠OAD，再由OA=OD，证出∠OAD=∠ADO，根据等量代换得出∠CAD=∠ADO，就可证明AC∥OD，由∠C=90°，得出OD⊥BC，即可证得结论。
（2）观察图形可知线段BD、BE与劣弧DE所围成的图形面积=△OBD的面积-扇形DOE的面积，根据已知先求出OD和BD的长，及圆心角∠DOE的度数，就可求出△OBD的面积和扇形DOE的面积，即可求出结果。
【考点精析】利用勾股定理的概念和扇形面积计算公式对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．
