��Ŀ����
����Ŀ����������Ҫ���������⣮
��1���벹ȫ������ʽ��2x2��4x��0�Ľ⼯�Ĺ��̣�
�ٹ��캯��������ͼ���ݲ���ʽ����������κ���y=��2x2��4x���������������ϵ�У�ͼ1���������κ���y=��2x2��4x��ͼ��ֻ����ͼ�ɣ���
����ý�㣬��ʾ���裬��y=0ʱ����÷��̩�2x2��4x=0�Ľ�Ϊ�� �������þ���߱�ʾ������y=��2x2��4xͼ����y��0�IJ��֣�
�۽���ͼ��д���⼯��������ʾͼ�ɵò���ʽ��2x2��4x��0�Ľ⼯Ϊ��2��x��0����������������һԪһ�β���ʽ�⼯�Ĺ��̣���ʽx2��2x+1��4�Ľ⼯��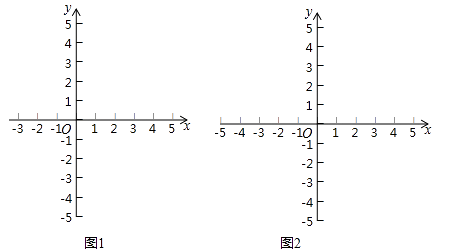
���𰸡�
��1���⣺��ͼ��ʾ��
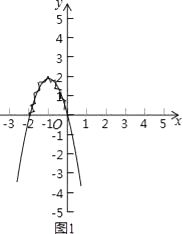
��x1=0��x2=��2����3��x��3��x�ܩ�1��
�ۺ���y=x2��2x+1��ͼ���ǣ�
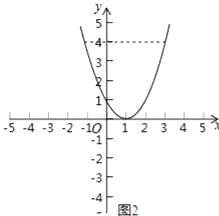
��y=4ʱ��x2��2x+1=4����ã�x1=3��x2=��1��
��ʽ�Ľ⼯�ǣ�x��3��x�ܩ�1��
���������ڷ��̩�2x2��4x=0����2x��x+2��=0��
��ã�x1=0��x2=��2��
�̵Ľ���x1=0��x2=��2��
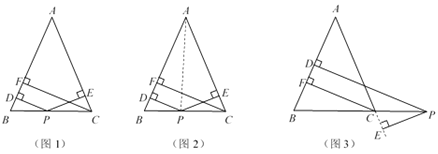
ͼ����ͼ1��
��������ʽ�ֽⷨ����dz��Ľ⣻�ٻ���y=��2x2��4x��ͼ�۲캯��ͼ���þ���߱�ʾ��y��0�IJ��֡�
�����������x2��2x+1=4�Ľ⣬�ٻ�������y=x2��2x+1��ͼ���ٹ۲캯��ͼ����y��4ʱ�Ա�����ȡֵ��Χ�����Ȼ���y=x2-2x-3���ٹ۲�y��0ʱ�Ա�����ȡֵ��Χ��

 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�