题目内容
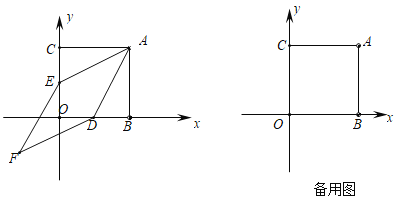
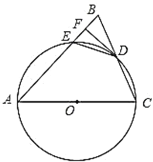
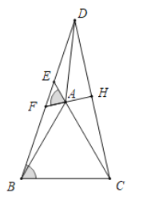
【题目】如图,![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 与点
与点![]() 分别位于直线
分别位于直线![]() 的两侧,且
的两侧,且![]() ,连接
,连接![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,
,
①当![]() 时,设
时,设![]() (其中
(其中![]() 表示
表示![]() 的面积,
的面积,![]() 表示
表示![]() 的面积),求
的面积),求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
②当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长.
的长.
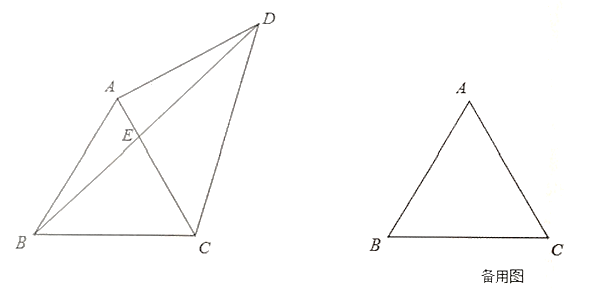
【答案】(1)线段![]() 的长是
的长是![]() ;(2)①
;(2)①![]() ;②AE=1或
;②AE=1或![]() .
.
【解析】
(1)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,设
,设![]() ,则
,则![]() ,根据BG=EG构建方程求出x即可得出答案;
,根据BG=EG构建方程求出x即可得出答案;
(2)①证明△AEF∽△BEC,可得![]() ,由此构建关系式即可解决问题.
,由此构建关系式即可解决问题.
②分两种情形:当∠CAD<120°时,当120°<∠CAD<180°时,分别得出方程求解即可解决问题.
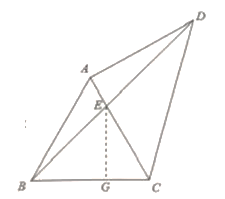
解:(1)∵![]() 是等边三角形,且
是等边三角形,且![]() ,
,
∴![]() ,
,![]() ,
,
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴线段![]() 的长是
的长是![]() ;
;
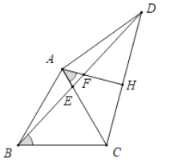
(2)①当∠CAD<120°时,
设∠ABD=![]() ,则∠BDA=
,则∠BDA=![]() ,∠DAC=∠BAD-∠BAC=120°-2
,∠DAC=∠BAD-∠BAC=120°-2![]() ,
,
∵AD=AC,AH⊥CD,
∴∠CAF=![]() ∠DAC=60°-
∠DAC=60°-![]() ,
,
∵∠AEF=60°+![]() ,
,
∴∠AFE=60°,
∴∠AFE=∠ACB,
∵∠AEF=∠BEC,
∴△AEF∽△BEC
∴![]() ,
,
由(1)得在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
②
![]() ,则有
,则有![]() ,
,
整理,得3x2+x-2=0
解得x=![]() 或-1(舍去)
或-1(舍去)
∴AE=![]()
当120°<∠CAD<180°时,
同理可得![]() ,
,
当![]() 时,则有
时,则有![]() ,
,
整理,得3x2-x-2=0
解得x=-![]() (舍去)或1,
(舍去)或1,
∴AE=1
综上所述,AE=1或![]() .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.
【题目】为了解某地区企业信息化发展水平,从该地区中随机抽取50家企业调研,针对体现企业信息化发展水平的A和B两项指标进行评估,获得了它们的成绩(十分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.A项指标成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
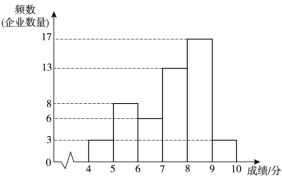
b.A项指标成绩在![]() 这一组的是:
这一组的是:
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c.![]() 两项指标成绩的平均数、中位数、众数如下:
两项指标成绩的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
A项指标成绩 | 7.37 | m | 8.2 |
B项指标成绩 | 7.21 | 7.3 | 8 |
根据以上信息,回答下列问题:
(1)写出表中m的值
(2)在此次调研评估中,某企业A项指标成绩和B项指标成绩都是7.5分,该企业成绩排名更靠前的指标是______________(填“A”或“B”),理由是_____________;
(3)如果该地区有500家企业,估计A项指标成绩超过7.68分的企业数量.
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下:
频数分布表
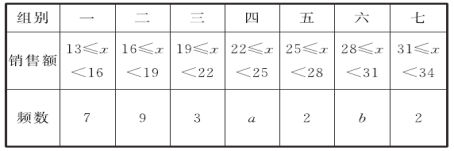
数据分析表
平均数 | 众数 | 中位数 |
20.3 | c | 18 |
请根据以上信息解答下列问题:
(1)填空:a=____,b=_____,c=_____;
(2)若将月销售额不低于25万元确定为销售目标,则有______位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.