题目内容
(本小题满分6分)
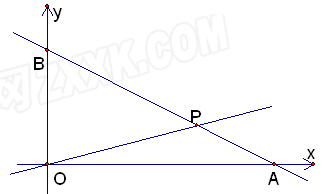
在如图所示的直角坐标系中,O为原点,直线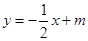 与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且
与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且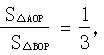 ,试求点P的坐标.
,试求点P的坐标.
在如图所示的直角坐标系中,O为原点,直线
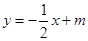 与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且
与x轴、y轴分别交于A、B两点,且点B的坐标为(0,8).(1)求m的值;(2)设直线OP与线段AB相交于P点,且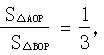 ,试求点P的坐标.
,试求点P的坐标.
(1) m=8 ……………………………2分
(2) (12,2) ……………………………4分
(2) (12,2) ……………………………4分
分析:
(1)根据B点的坐标即可求出m的值;
(2)根据△AOP和△BOP的面积之比求出AP与BP的比值,再过点P做PC⊥OA垂足为点C,求出OC的长即可求出点P的坐标;
解答:
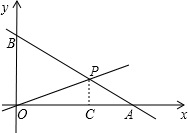
(1)∵直线y=-1/2x+m与y轴交于B点,点B的坐标为(0,8),
∴m=8。
(2)∵S△AOP / S△BOP=1/3,
∴AP/BP=1/3。
过点P做PC⊥OA垂足为点C,
则AC/OC=AP/BP=1/3
∵直线y=-1/2x+8与x轴交于A点,
∴点A的坐标为(16,0).
∴OA=16
∴OC=16×3/4=12
∴点P的横坐标为12。
∵点P在直线y=-1/2x+8上
∴点P的纵坐标为y=-1/2×12+8=2,
∴点P的坐标为(12,2)。
点评:本题主要考查了一次函数的图象和性质,解题时要注意有关知识的综合应用。

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目

 (个)与销售时间
(个)与销售时间 (天)之间有如下关系:
(天)之间有如下关系: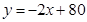 (
(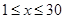 ,且
,且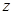 (元/个)与销售时间
(元/个)与销售时间 (元)与销售时间
(元)与销售时间 而日销售量就比9月30日提高了
而日销售量就比9月30日提高了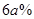 (其中
(其中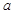 为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求
为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求 (参考数据:
(参考数据: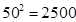 ,
,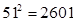 ,
, )
) 拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
拟台球游戏,为简单起见,约定:①每个球袋视为一个点,如果不遇到障碍,各球均沿直线前进;②A球击B球,意味着B球在A球前进的路线上,且B球被撞击后沿A球原来的方向前进;③球撞击桌边后的反弹角度等于入射角度,(如图中∠β=∠a)如图所示,设桌边只剩下白球,A,6号球B。
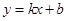 经过点(k,3)和(1,k),则k的值为( )
经过点(k,3)和(1,k),则k的值为( )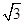
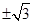
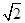
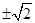


 分公司,其中40瓶给甲公司,60瓶给乙公司,且都能卖完,两公司的利润(元)如下表.
分公司,其中40瓶给甲公司,60瓶给乙公司,且都能卖完,两公司的利润(元)如下表. 方案,并将各种方案设计出来.
方案,并将各种方案设计出来.